What Is The Lcm Of 10 15
Juapaving
Apr 04, 2025 · 5 min read
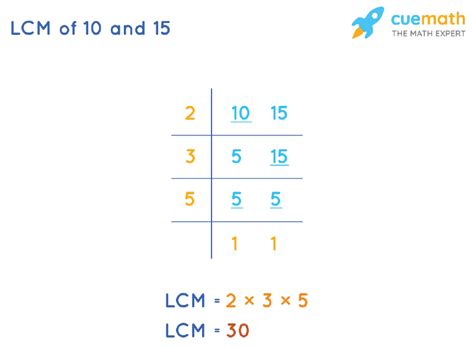
Table of Contents
What is the LCM of 10 and 15? A Deep Dive into Least Common Multiples
Finding the least common multiple (LCM) of two numbers is a fundamental concept in mathematics with wide-ranging applications in various fields, from simplifying fractions to solving complex problems in physics and engineering. This article provides a comprehensive guide to understanding LCM, specifically focusing on finding the LCM of 10 and 15. We will explore different methods, delve into the underlying theory, and illustrate the practical relevance of this seemingly simple calculation.
Understanding Least Common Multiples (LCM)
The least common multiple (LCM) of two or more integers is the smallest positive integer that is divisible by all the integers. In simpler terms, it's the smallest number that all the given numbers can divide into without leaving a remainder. For instance, the LCM of 2 and 3 is 6, because 6 is the smallest number divisible by both 2 and 3.
Key Characteristics of LCM:
- Positive Integer: The LCM is always a positive integer.
- Smallest Multiple: It's the smallest number that satisfies the divisibility condition.
- Divisibility: All the given numbers are factors of the LCM.
Methods for Finding the LCM of 10 and 15
Several methods exist for calculating the LCM of two numbers. Let's explore the most common ones, applying them to find the LCM of 10 and 15.
1. Listing Multiples Method
This method involves listing the multiples of each number until a common multiple is found. The smallest common multiple is the LCM.
- Multiples of 10: 10, 20, 30, 40, 50, 60...
- Multiples of 15: 15, 30, 45, 60, 75...
As you can see, the smallest common multiple of 10 and 15 is 30. Therefore, the LCM(10, 15) = 30. This method is straightforward for smaller numbers but becomes less efficient for larger numbers.
2. Prime Factorization Method
This is a more systematic and efficient method, especially for larger numbers. It involves finding the prime factorization of each number and then constructing the LCM using the highest powers of all prime factors present.
- Prime factorization of 10: 2 x 5
- Prime factorization of 15: 3 x 5
To find the LCM, we take the highest power of each prime factor present in the factorizations:
- Highest power of 2: 2¹ = 2
- Highest power of 3: 3¹ = 3
- Highest power of 5: 5¹ = 5
Multiplying these highest powers together gives us the LCM: 2 x 3 x 5 = 30
Therefore, the LCM(10, 15) = 30. This method is generally preferred for its efficiency and systematic approach.
3. Using the Greatest Common Divisor (GCD)
The LCM and GCD (greatest common divisor) of two numbers are related through a simple formula:
LCM(a, b) x GCD(a, b) = a x b
Where 'a' and 'b' are the two numbers. First, we need to find the GCD of 10 and 15.
- Factors of 10: 1, 2, 5, 10
- Factors of 15: 1, 3, 5, 15
The greatest common factor of 10 and 15 is 5. Therefore, GCD(10, 15) = 5.
Now, we can use the formula:
LCM(10, 15) x 5 = 10 x 15
LCM(10, 15) = (10 x 15) / 5 = 30
Therefore, the LCM(10, 15) = 30. This method is particularly useful when dealing with larger numbers where finding the prime factorization might be more challenging.
Applications of LCM
The concept of LCM finds extensive applications in various areas:
1. Fraction Addition and Subtraction
When adding or subtracting fractions with different denominators, finding the LCM of the denominators is crucial. The LCM becomes the common denominator, simplifying the addition or subtraction process.
For example, to add 1/10 and 1/15, we find the LCM of 10 and 15, which is 30. We then rewrite the fractions with a denominator of 30:
(3/30) + (2/30) = 5/30 = 1/6
2. Scheduling and Time Management
LCM is used in scheduling problems to find the time when events will occur simultaneously. For instance, if two buses arrive at a stop every 10 and 15 minutes respectively, the LCM (30 minutes) determines when both buses will arrive together.
3. Pattern Recognition and Cycles
In scenarios involving repeating patterns or cycles, the LCM helps identify when the patterns will coincide. This has applications in various fields, including music, physics, and computer science.
4. Gear Ratios and Mechanical Systems
In mechanical engineering, LCM is used to calculate gear ratios and synchronize rotating parts in machinery to ensure smooth operation.
5. Number Theory and Abstract Algebra
LCM is a fundamental concept in number theory, forming the basis for many advanced mathematical theorems and concepts.
Beyond the Basics: Extending LCM Concepts
The principles of LCM extend beyond finding the LCM of just two numbers. We can find the LCM of three or more numbers by applying the prime factorization method or iterative application of the two-number LCM method.
For example, to find the LCM of 10, 15, and 20:
- Prime factorization of 10: 2 x 5
- Prime factorization of 15: 3 x 5
- Prime factorization of 20: 2² x 5
The LCM would be 2² x 3 x 5 = 60
Conclusion: The Importance of Understanding LCM
Understanding and mastering the calculation of the least common multiple is essential for success in various mathematical and scientific endeavors. While the example of finding the LCM of 10 and 15 might seem trivial, the underlying principles and methods are applicable to much more complex scenarios. This article has provided a detailed explanation of different methods, highlighting their strengths and weaknesses, and showcasing the practical relevance of LCM across various disciplines. By understanding the concepts presented here, you'll be equipped to confidently tackle LCM problems and apply this fundamental mathematical skill to a wide range of applications. Remember to choose the method that best suits your needs and the complexity of the numbers involved. The prime factorization method is generally recommended for its efficiency and systematic nature, especially when dealing with larger numbers or multiple numbers simultaneously.
Latest Posts
Latest Posts
-
Number Of Valence Electrons In Mg
Apr 11, 2025
-
Is Lagging Strand 3 To 5
Apr 11, 2025
-
What Is Ex Situ And In Situ Conservation
Apr 11, 2025
-
How Are Photosynthesis And Cellular Respiration Related Apex
Apr 11, 2025
-
Least Common Multiple Of 2 And 10
Apr 11, 2025
Related Post
Thank you for visiting our website which covers about What Is The Lcm Of 10 15 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.