What Is The Lcm For 3 And 8
Juapaving
Apr 03, 2025 · 5 min read
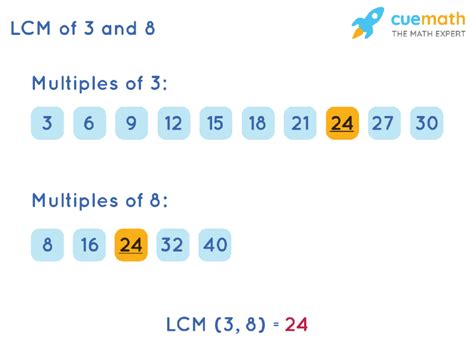
Table of Contents
Unveiling the LCM: A Deep Dive into Finding the Least Common Multiple of 3 and 8
Finding the least common multiple (LCM) might seem like a simple arithmetic task, but understanding the underlying concepts and exploring different methods can reveal surprising depth and applicability across various mathematical fields. This article delves into the specifics of determining the LCM of 3 and 8, expanding upon the calculation to explore broader concepts of number theory and their real-world applications. We'll move beyond a simple answer and explore why this seemingly basic concept is so crucial.
What is the Least Common Multiple (LCM)?
The least common multiple (LCM) of two or more integers is the smallest positive integer that is divisible by all the integers. In simpler terms, it's the smallest number that contains all the numbers as factors. Think of it as the smallest common ground where all the numbers meet. For example, the LCM of 2 and 3 is 6 because 6 is the smallest positive integer divisible by both 2 and 3.
Methods for Calculating the LCM
Several methods exist for calculating the LCM, each with its own advantages and disadvantages. We'll explore the most common approaches, focusing on how they apply to finding the LCM of 3 and 8.
1. Listing Multiples Method
This is the most intuitive method, especially for smaller numbers. We list the multiples of each number until we find the smallest common multiple.
- Multiples of 3: 3, 6, 9, 12, 15, 18, 21, 24, 27, 30...
- Multiples of 8: 8, 16, 24, 32, 40...
Notice that the smallest number appearing in both lists is 24. Therefore, the LCM of 3 and 8 is 24.
This method is straightforward for small numbers but becomes cumbersome for larger numbers. Imagine trying to find the LCM of 147 and 252 using this method!
2. Prime Factorization Method
This method uses the prime factorization of each number. Prime factorization involves expressing a number as a product of its prime factors (numbers divisible only by 1 and themselves).
- Prime factorization of 3: 3 (3 is a prime number)
- Prime factorization of 8: 2 x 2 x 2 = 2³
To find the LCM using prime factorization, we take the highest power of each prime factor present in the factorizations and multiply them together.
In this case, the prime factors are 2 and 3. The highest power of 2 is 2³ (from the factorization of 8), and the highest power of 3 is 3¹ (from the factorization of 3).
Therefore, LCM(3, 8) = 2³ x 3 = 8 x 3 = 24
This method is more efficient for larger numbers because it avoids the tedious task of listing multiples.
3. Greatest Common Divisor (GCD) Method
The LCM and the greatest common divisor (GCD) are closely related. The GCD is the largest number that divides both numbers without leaving a remainder. The relationship between LCM and GCD is given by the formula:
LCM(a, b) = (|a x b|) / GCD(a, b)
First, we need to find the GCD of 3 and 8. Since 3 is a prime number and 8 is not divisible by 3, the GCD of 3 and 8 is 1.
Now, we can use the formula:
LCM(3, 8) = (3 x 8) / GCD(3, 8) = 24 / 1 = 24
This method is efficient, especially when dealing with larger numbers where finding the GCD might be easier than directly calculating the LCM. Algorithms like the Euclidean algorithm are highly efficient for finding the GCD of large numbers.
Applications of LCM in Real-World Scenarios
The seemingly simple concept of LCM has far-reaching applications in various fields:
-
Scheduling: Imagine two buses leaving a station at different intervals. One bus leaves every 3 hours, and another leaves every 8 hours. The LCM (24 hours) tells us when both buses will depart at the same time again. This principle extends to various scheduling problems, from factory production lines to appointment scheduling.
-
Fractions: When adding or subtracting fractions, finding the LCM of the denominators is crucial to obtain a common denominator. This simplification simplifies calculations and makes it easier to compare fractions.
-
Music: Musical rhythms and harmonies are often based on LCM. The LCM determines when different musical phrases or patterns will coincide, creating rhythmic complexity and consonance.
-
Construction & Engineering: In construction, LCM is used in determining the lengths of materials needed to avoid waste. For instance, if you need to cut pieces of wood of length 3 units and 8 units, using multiples of their LCM (24 units) ensures minimal wastage.
-
Computer Science: LCM is utilized in various algorithms and data structures, particularly those involving cyclical processes or synchronization of events.
Expanding on the Concept: Beyond Two Numbers
The methods described above can be extended to find the LCM of more than two numbers. The prime factorization method is particularly useful in these cases. For example, to find the LCM of 3, 8, and 5:
-
Prime Factorization:
- 3 = 3
- 8 = 2³
- 5 = 5
-
Highest Powers: The highest powers of the prime factors are 2³, 3, and 5.
-
LCM: LCM(3, 8, 5) = 2³ x 3 x 5 = 8 x 3 x 5 = 120
Conclusion: The Significance of a Simple Calculation
While finding the LCM of 3 and 8 might seem trivial, the underlying principles and methods have wide-ranging applications across various domains. Understanding the different approaches to calculating the LCM, and its relationship to the GCD, provides a strong foundation in number theory and its practical implications. This knowledge empowers you to tackle more complex mathematical problems and apply these concepts to real-world scenarios, making you a more versatile problem-solver. From scheduling events to optimizing resource allocation, the LCM continues to be a powerful tool in numerous fields. The seemingly simple answer of 24 for the LCM of 3 and 8 opens the door to a world of mathematical possibilities.
Latest Posts
Latest Posts
-
Difference Between Real And Natural Numbers
Apr 04, 2025
-
What Energy Conversion Occurs During Photosynthesis
Apr 04, 2025
-
How Are Fish Able To Live In A Frozen Lake
Apr 04, 2025
-
How Many Minutes Are In 9 Hours
Apr 04, 2025
-
What Are The Components Of Atp
Apr 04, 2025
Related Post
Thank you for visiting our website which covers about What Is The Lcm For 3 And 8 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
