What Is The Lcm For 3 And 5
Juapaving
Apr 04, 2025 · 5 min read
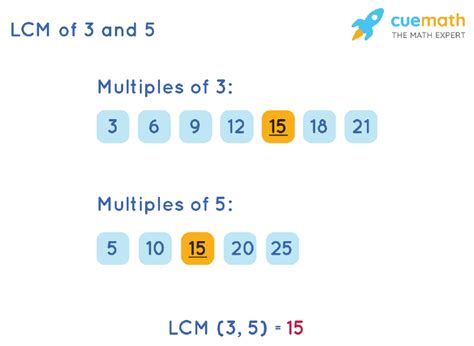
Table of Contents
What is the LCM for 3 and 5? A Deep Dive into Least Common Multiples
Finding the least common multiple (LCM) is a fundamental concept in mathematics, particularly in arithmetic and number theory. It's a skill that extends beyond basic calculations and finds application in various fields, from scheduling tasks to simplifying fractions and solving complex equations. This article will thoroughly explore the LCM of 3 and 5, providing a comprehensive understanding of the concept itself, various methods to calculate it, and showcasing its real-world relevance.
Understanding Least Common Multiples (LCM)
The least common multiple (LCM) of two or more integers is the smallest positive integer that is a multiple of all the integers. In simpler terms, it's the smallest number that can be divided evenly by all the given numbers without leaving a remainder. Understanding multiples is crucial: a multiple of a number is the product of that number and any integer. For example, multiples of 3 are 3, 6, 9, 12, 15, 18, and so on.
Let's delve into the specifics of finding the LCM for 3 and 5. We'll explore several methods, each offering a different approach to solving this seemingly simple problem, which will solidify the understanding of the concept itself.
Method 1: Listing Multiples
This is the most straightforward method, particularly useful for smaller numbers like 3 and 5. We list the multiples of each number until we find the smallest multiple that appears in both lists.
Multiples of 3: 3, 6, 9, 12, 15, 18, 21, 24, 27, 30...
Multiples of 5: 5, 10, 15, 20, 25, 30, 35...
Notice that 15 appears in both lists. However, 30 also appears in both lists. The least common multiple is the smallest number that appears in both sets, making 15 the LCM of 3 and 5.
Method 2: Prime Factorization
This method is more efficient for larger numbers and provides a deeper understanding of the underlying mathematical principles. It involves breaking down each number into its prime factors. Prime factors are prime numbers (numbers divisible only by 1 and themselves) that multiply to give the original number.
- Prime factorization of 3: 3 (3 is itself a prime number)
- Prime factorization of 5: 5 (5 is also a prime number)
To find the LCM using prime factorization, we consider the highest power of each prime factor present in the numbers. In this case:
- The highest power of 3 is 3¹ = 3
- The highest power of 5 is 5¹ = 5
Multiply these highest powers together: 3 * 5 = 15. Therefore, the LCM of 3 and 5 is 15.
Method 3: Using the Formula (for two numbers)
A formula exists specifically for calculating the LCM of two numbers, given their greatest common divisor (GCD). The GCD is the largest number that divides both numbers without leaving a remainder. The formula is:
LCM(a, b) = (|a * b|) / GCD(a, b)
Where:
- a and b are the two numbers
- |a * b| represents the absolute value of the product of a and b
- GCD(a, b) is the greatest common divisor of a and b
Let's apply this to 3 and 5:
- GCD(3, 5) = 1 (3 and 5 have no common divisors other than 1)
- LCM(3, 5) = (3 * 5) / 1 = 15
This confirms, once again, that the LCM of 3 and 5 is 15.
Method 4: Visual Representation - Venn Diagram
While not a direct calculation method, a Venn diagram can help visualize the prime factors and the relationship between the numbers and their LCM. Since 3 and 5 are both prime numbers, their Venn diagram would show two separate circles, each containing only its respective prime number. The LCM would be the product of the numbers in both circles, which is 3 * 5 = 15.
Real-World Applications of LCM
The LCM finds practical application in numerous scenarios:
-
Scheduling: Imagine two buses arrive at a stop; one every 3 minutes and the other every 5 minutes. The LCM (15 minutes) determines when both buses will arrive at the stop simultaneously.
-
Fraction Addition/Subtraction: To add or subtract fractions, you need a common denominator, which is the LCM of the denominators. For instance, adding 1/3 and 1/5 requires finding the LCM of 3 and 5 (which is 15), then converting the fractions to have a denominator of 15 before adding them.
-
Patterning and Cycles: In repetitive tasks or cyclical events, the LCM helps determine when events will align or repeat simultaneously.
-
Gear Ratios: In mechanics, gear ratios and synchronization often involve LCM calculations to determine efficient rotational speeds.
LCM of More Than Two Numbers
The methods described above can be extended to find the LCM of more than two numbers. Prime factorization becomes increasingly useful for larger sets of numbers. For instance, to find the LCM of 3, 5, and 7:
-
Prime Factorization:
- 3 = 3
- 5 = 5
- 7 = 7
-
Identify Highest Powers:
- Highest power of 3: 3¹ = 3
- Highest power of 5: 5¹ = 5
- Highest power of 7: 7¹ = 7
-
Multiply the Highest Powers: 3 * 5 * 7 = 105. The LCM of 3, 5, and 7 is 105.
Beyond the Basics: Exploring Advanced Concepts
The concept of LCM extends into more advanced mathematical fields. Understanding LCM lays the groundwork for:
-
Modular Arithmetic: LCM plays a vital role in solving congruences and understanding cyclical patterns in modular arithmetic.
-
Abstract Algebra: The concept of LCM is generalized in abstract algebra, particularly in ring theory.
-
Number Theory: LCM is fundamental in various theorems and proofs within number theory.
Conclusion: The Power of 15
We've explored multiple methods to calculate the LCM of 3 and 5, consistently arriving at the answer: 15. While this specific example might seem simple, understanding the different approaches and their underlying principles is crucial. The ability to find the least common multiple is not just a mathematical skill; it's a valuable tool applicable across various disciplines and essential for solving a broad range of problems. Mastering the LCM is a stepping stone to a more profound understanding of mathematics and its real-world applications. By understanding the multiple methods, from listing multiples to prime factorization and using the formula, you gain a comprehensive grasp of this fundamental concept, empowering you to tackle more complex mathematical challenges with confidence.
Latest Posts
Latest Posts
-
Water In Gas Form Is Called
Apr 04, 2025
-
Dna Replication Occurs Prior To Both Meiosis And Mitosis
Apr 04, 2025
-
4 Cubic Feet To Dry Quarts
Apr 04, 2025
-
Change The Decimal To A Percent 0 7
Apr 04, 2025
-
A Proton A Deuteron And An Alpha Particle Are Accelerated
Apr 04, 2025
Related Post
Thank you for visiting our website which covers about What Is The Lcm For 3 And 5 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
