What Is The Integral Of 3x
Juapaving
May 12, 2025 · 5 min read
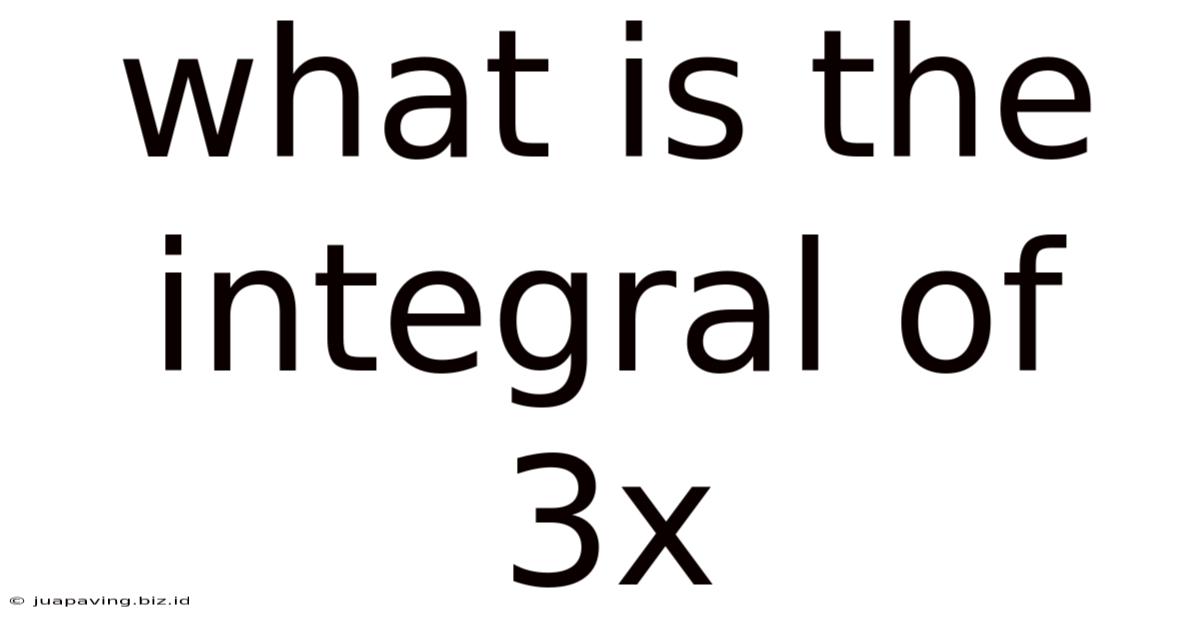
Table of Contents
What is the Integral of 3x? A Comprehensive Guide
The seemingly simple question, "What is the integral of 3x?", opens the door to a fundamental concept in calculus: integration. This seemingly straightforward problem allows us to explore various techniques and underlying principles, making it a perfect starting point for understanding this powerful mathematical tool. This comprehensive guide will delve deep into finding the integral of 3x, exploring different approaches, and highlighting the broader implications of this calculation within the realm of calculus.
Understanding Integration: The Antiderivative
Before diving into the specific integral of 3x, let's establish a solid foundation in integration. Integration, in its most basic form, is the reverse process of differentiation. Differentiation finds the instantaneous rate of change of a function, while integration finds the function whose derivative is the given function. This "reverse" function is called the antiderivative.
Consider a function, f(x). Its derivative, denoted as f'(x) or df/dx, represents the slope of the tangent line at any point on the graph of f(x). Integration, then, seeks to find the original function f(x) given its derivative f'(x).
The notation for indefinite integration is:
∫f(x) dx
where:
- ∫ is the integral symbol
- f(x) is the function to be integrated (the integrand)
- dx indicates that the integration is with respect to the variable x.
The result of indefinite integration is a family of functions, differing only by a constant. This is because the derivative of a constant is always zero. We denote this constant as "+C".
Calculating the Integral of 3x
Now, let's tackle the integral of 3x:
∫3x dx
We need to find a function whose derivative is 3x. Recall the power rule of differentiation:
d/dx (xⁿ) = nxⁿ⁻¹
The power rule's counterpart in integration is:
∫xⁿ dx = (xⁿ⁺¹)/(n+1) + C (where n ≠ -1)
Applying this rule to our problem, where n=1:
∫3x dx = 3∫x¹ dx = 3 * [(x¹⁺¹)/(1+1)] + C = 3 * (x²/2) + C = (3/2)x² + C
Therefore, the integral of 3x is (3/2)x² + C.
Verifying the Result through Differentiation
A crucial step in any integration problem is verification. We can check our answer by differentiating the result and seeing if it matches the original integrand. Let's differentiate (3/2)x² + C:
d/dx [(3/2)x² + C] = (3/2) * 2x + 0 = 3x
Since the derivative of (3/2)x² + C is indeed 3x, our integration is correct.
The Significance of the Constant of Integration, C
The constant of integration, "+C", is a critical component of indefinite integrals. It represents a family of functions, all of which have the same derivative. For instance:
- (3/2)x² + 1
- (3/2)x² - 5
- (3/2)x² + π
All these functions have the same derivative: 3x. The constant C accounts for the vertical shift of the graph; changing C simply shifts the entire curve up or down without altering its slope.
The value of C is determined only when we have additional information, such as a specific point the function must pass through (an initial condition). This leads to the concept of definite integrals.
Definite Integrals and the Fundamental Theorem of Calculus
While indefinite integrals give us a family of functions, definite integrals provide a numerical value. A definite integral is represented as:
∫[a,b] f(x) dx
where 'a' and 'b' are the limits of integration. The Fundamental Theorem of Calculus links definite and indefinite integrals:
∫[a,b] f(x) dx = F(b) - F(a)
where F(x) is the antiderivative of f(x).
Let's consider the definite integral of 3x from x=1 to x=3:
∫[1,3] 3x dx = [(3/2)x²]₃¹ = [(3/2)(3)²] - [(3/2)(1)²] = (27/2) - (3/2) = 12
This means the area under the curve y = 3x between x=1 and x=3 is 12 square units.
Applications of Integration: Beyond the Basics
The seemingly simple integral of 3x has far-reaching applications in various fields. It forms the foundation for solving more complex integration problems and plays a critical role in:
- Physics: Calculating displacement from velocity, finding work done by a force, and determining the center of mass of objects.
- Engineering: Analyzing stress and strain in structures, determining fluid flow rates, and solving problems in heat transfer.
- Economics: Modeling growth and decay, calculating present value and future value of investments, and analyzing consumer behavior.
- Probability and Statistics: Finding probabilities and expected values for continuous random variables.
Advanced Integration Techniques
While the integral of 3x is easily solved using the power rule, more complex functions require advanced techniques, including:
- Integration by substitution (u-substitution): Used for simplifying integrals by substituting a new variable.
- Integration by parts: A technique based on the product rule of differentiation, useful for integrating products of functions.
- Partial fraction decomposition: Used for integrating rational functions by breaking them down into simpler fractions.
- Trigonometric substitutions: Used for integrals involving trigonometric functions.
Conclusion: Mastering the Fundamentals
Understanding the integral of 3x provides a solid foundation for tackling more complex integration problems. This seemingly basic calculation underpins numerous applications across various disciplines, highlighting the crucial role of integration in mathematics and its impact on our understanding of the world around us. Mastering the fundamentals of integration, including the power rule, the constant of integration, and the relationship between definite and indefinite integrals, is essential for anyone seeking to delve deeper into the world of calculus. By grasping these core concepts, one can confidently navigate more intricate integration problems and unlock the powerful applications of this vital mathematical tool. Remember to always verify your results by differentiation, ensuring accuracy and deepening your understanding of the relationship between integration and differentiation.
Latest Posts
Latest Posts
-
How Many Vertices Does A Hexagonal Pyramid Have
May 12, 2025
-
Action Words That Start With G
May 12, 2025
-
The Atomic Number Of Phosphorus Is
May 12, 2025
-
What Ratios Are Equivalent To 3 4
May 12, 2025
-
Does Phosphorus Have A Gaseous Phase
May 12, 2025
Related Post
Thank you for visiting our website which covers about What Is The Integral Of 3x . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.