What Is The Gcf Of 49
Juapaving
Mar 24, 2025 · 6 min read
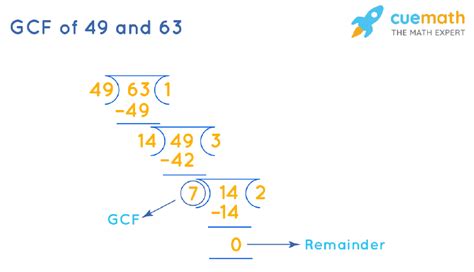
Table of Contents
- What Is The Gcf Of 49
- Table of Contents
- What is the GCF of 49? A Deep Dive into Greatest Common Factors
- Understanding Greatest Common Factors (GCF)
- Finding the GCF of 49: A Simple Case
- Methods for Finding the GCF
- 1. Prime Factorization Method
- 2. Listing Factors Method
- 3. Euclidean Algorithm
- Applications of GCF
- 1. Simplifying Fractions
- 2. Solving Algebraic Equations
- 3. Geometry and Measurement
- 4. Number Theory
- 5. Computer Science and Cryptography
- 6. Music Theory
- Conclusion: The Significance of GCF
- Latest Posts
- Latest Posts
- Related Post
What is the GCF of 49? A Deep Dive into Greatest Common Factors
Finding the greatest common factor (GCF) of a number might seem like a simple arithmetic task, but understanding the underlying concepts unlocks a world of mathematical applications. This article will explore the GCF of 49, explain the process of finding GCFs in general, and delve into its significance in various mathematical contexts. We'll cover different methods, including prime factorization and the Euclidean algorithm, providing a comprehensive understanding of this fundamental concept.
Understanding Greatest Common Factors (GCF)
The greatest common factor (GCF), also known as the greatest common divisor (GCD), is the largest positive integer that divides each of the integers without leaving a remainder. In simpler terms, it's the biggest number that perfectly divides all the numbers in a given set. For example, the GCF of 12 and 18 is 6, because 6 is the largest number that divides both 12 and 18 evenly.
This concept is crucial in various areas of mathematics, from simplifying fractions to solving algebraic equations and beyond. Its applications extend to computer science, cryptography, and even music theory.
Finding the GCF of 49: A Simple Case
The number 49 presents a relatively straightforward case. To find its GCF, we need to consider its factors – the numbers that divide 49 without leaving a remainder.
The factors of 49 are: 1, 7, and 49.
Since 49 is a prime number squared (7 x 7), its only factors are 1, 7, and 49 itself. Therefore, if we are considering the GCF of 49 and another number, the GCF will be either 1, 7, or 49, depending on the other number.
- If we want the GCF of 49 and a number that doesn't share any factors with 49 (other than 1), the GCF will be 1. For example, the GCF of 49 and 12 is 1.
- If we want the GCF of 49 and a multiple of 7, the GCF will be a multiple of 7. For example, the GCF of 49 and 21 is 7 (because 21 = 3 x 7).
- If we want the GCF of 49 and 49, the GCF will be 49. This is because 49 is a factor of itself.
Therefore, the GCF of 49 alone is 49, because a number's greatest common factor with itself is always the number itself. However, the GCF becomes relevant when considering 49 in relation to other numbers.
Methods for Finding the GCF
While the GCF of 49 is easily determined through observation due to 49's unique properties, let's explore more general methods applicable to finding the GCF of any set of numbers.
1. Prime Factorization Method
This method involves breaking down each number into its prime factors – the prime numbers that multiply together to give the original number. The GCF is then found by identifying the common prime factors and multiplying them together.
Let's illustrate this with an example: Find the GCF of 49 and 98.
- Prime factorization of 49: 7 x 7 = 7²
- Prime factorization of 98: 2 x 7 x 7 = 2 x 7²
The common prime factors are 7 and 7. Therefore, the GCF of 49 and 98 is 7 x 7 = 49.
2. Listing Factors Method
This method involves listing all the factors of each number and then identifying the largest common factor.
Let's use the same example: Find the GCF of 49 and 98.
- Factors of 49: 1, 7, 49
- Factors of 98: 1, 2, 7, 14, 49, 98
The common factors are 1, 7, and 49. The greatest of these is 49, so the GCF of 49 and 98 is 49. This method is most effective for smaller numbers.
3. Euclidean Algorithm
This method is particularly efficient for larger numbers. It uses repeated division until the remainder is 0. The last non-zero remainder is the GCF.
Let's find the GCF of 49 and 112 using the Euclidean algorithm:
- Divide the larger number (112) by the smaller number (49): 112 ÷ 49 = 2 with a remainder of 14.
- Replace the larger number with the smaller number (49) and the smaller number with the remainder (14): 49 ÷ 14 = 3 with a remainder of 7.
- Repeat: 14 ÷ 7 = 2 with a remainder of 0.
Since the last non-zero remainder is 7, the GCF of 49 and 112 is 7.
Applications of GCF
The concept of the greatest common factor has wide-ranging applications across various mathematical domains and beyond:
1. Simplifying Fractions
GCF is fundamental to simplifying fractions. To simplify a fraction, you divide both the numerator and the denominator by their GCF. For example, to simplify the fraction 49/98, you would divide both by their GCF (49), resulting in the simplified fraction 1/2.
2. Solving Algebraic Equations
GCF plays a crucial role in factoring algebraic expressions, which is essential for solving various types of equations. Finding the GCF of terms allows you to simplify and solve equations more efficiently.
3. Geometry and Measurement
GCF is used in geometry when dealing with problems involving finding the dimensions of shapes or calculating areas and volumes. For example, when determining the side lengths of a square that can perfectly tile a rectangular area, the GCF of the rectangle's dimensions is crucial.
4. Number Theory
GCF is a central concept in number theory, forming the foundation for many theorems and algorithms. It's vital in understanding the relationships between numbers and their divisors.
5. Computer Science and Cryptography
GCF, and specifically the Euclidean algorithm for finding it, has significant applications in computer science, especially in cryptography. Algorithms like RSA encryption rely heavily on the efficient computation of GCFs for their security.
6. Music Theory
Surprisingly, GCF even finds its way into music theory. It's used in determining the relationships between musical intervals and harmonies.
Conclusion: The Significance of GCF
The seemingly simple concept of the greatest common factor has far-reaching implications across various fields. While the GCF of 49, when considered in isolation, is simply 49, the importance lies in its application when determining the GCF of 49 with other numbers. Understanding the methods to calculate GCF – whether through prime factorization, listing factors, or the Euclidean algorithm – empowers us to tackle complex mathematical problems and appreciate the interconnectedness of seemingly disparate mathematical concepts. Its significance extends far beyond basic arithmetic, impacting areas like algebra, geometry, number theory, and even computer science. Mastering the concept of GCF is not just about understanding a single calculation, but about unlocking a deeper understanding of number relationships and their importance in diverse fields.
Latest Posts
Latest Posts
-
Is Electric Charge A Vector Quantity
Mar 27, 2025
-
Of The Halogens Which Has The Smallest Radius
Mar 27, 2025
-
How Many Kilos Is 200 Lbs
Mar 27, 2025
-
Which Of The Following Is Not Required For Transcription
Mar 27, 2025
-
Words That Start With A H
Mar 27, 2025
Related Post
Thank you for visiting our website which covers about What Is The Gcf Of 49 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
