What Is The Difference Between A Rhombus And Parallelogram
Juapaving
Mar 21, 2025 · 5 min read
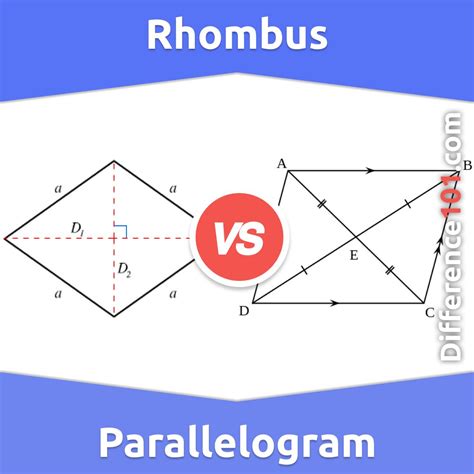
Table of Contents
What's the Difference Between a Rhombus and a Parallelogram? A Comprehensive Guide
Understanding the differences between geometric shapes like rhombuses and parallelograms can seem daunting at first, but with a clear explanation and some helpful visuals, it becomes much simpler. Both shapes belong to the broader family of quadrilaterals – four-sided polygons – but possess unique characteristics that set them apart. This article will delve into the specifics of each shape, highlighting their similarities and critically examining their differences. We’ll explore their properties, angles, diagonals, and even touch upon their applications in real-world scenarios.
Defining Parallelograms
A parallelogram is a quadrilateral where opposite sides are parallel and equal in length. This fundamental property dictates many other characteristics of the shape. Imagine pushing a rectangle; you’ll still have parallel opposite sides, though the angles might change. This illustrates the flexibility inherent in parallelograms.
Key Properties of Parallelograms:
- Opposite sides are parallel: This is the defining characteristic. Lines extended from opposite sides will never intersect.
- Opposite sides are congruent (equal in length): This is a direct consequence of the parallel sides.
- Opposite angles are congruent: The angles opposite each other are always equal in measure.
- Consecutive angles are supplementary: This means that any two angles next to each other add up to 180 degrees.
- Diagonals bisect each other: The diagonals intersect at a point that divides each diagonal into two equal segments.
Delving into Rhombuses
A rhombus, often called a diamond, is a special type of parallelogram. This means it inherits all the properties of a parallelogram, but adds a crucial extra feature: all four sides are equal in length. This additional constraint significantly impacts the shape's overall geometry. Think of it as a parallelogram with the extra condition of equal side lengths.
Unique Properties of Rhombuses:
- All sides are congruent (equal in length): This is the defining characteristic that distinguishes a rhombus from a general parallelogram.
- Opposite sides are parallel: This is inherited from its parallelogram lineage.
- Opposite angles are congruent: This too, is inherited.
- Consecutive angles are supplementary: Again, this property is inherited.
- Diagonals bisect each other at right angles: This is a crucial difference. While parallelogram diagonals bisect each other, they only bisect at right angles in a rhombus.
- Diagonals bisect the angles: Each diagonal divides its respective angles into two equal halves.
Comparing Parallelograms and Rhombuses: A Table Summary
To crystallize the distinctions, let's summarize the key differences in a table:
| Feature | Parallelogram | Rhombus |
|---|---|---|
| Sides | Opposite sides are equal and parallel | All four sides are equal and parallel |
| Angles | Opposite angles are equal; consecutive angles are supplementary | Opposite angles are equal; consecutive angles are supplementary; diagonals bisect angles |
| Diagonals | Bisect each other | Bisect each other at right angles; bisect angles |
| Shape | Can be rectangular, square, or oblique | Always has equal sides; can be a square |
Visual Representations
Visual aids are invaluable for understanding geometric concepts. Imagine visualizing a parallelogram that is stretched or compressed. The opposite sides remain parallel and equal, fulfilling the parallelogram criteria. However, if you were to further constrain this parallelogram so that all four sides become equal in length, you would obtain a rhombus.
Real-world Applications
Both parallelograms and rhombuses find applications in various fields:
-
Parallelograms: You can find parallelogram shapes in everyday objects like books, windows, and even some building designs. Their stability makes them useful in construction and design.
-
Rhombuses: The rhombus shape is prominent in various contexts, including:
- Crystalline structures: Certain crystals exhibit rhombic structures at the atomic level.
- Tessellations: Rhombuses can tile a plane perfectly, creating aesthetically pleasing patterns in art and design.
- Artwork and design: The distinctive shape features prominently in logos, graphics, and artistic representations.
Squares and Rectangles: Special Cases
It's important to note that squares and rectangles are special cases of both parallelograms and rhombuses.
-
Square: A square is a rhombus with right angles (and therefore also a rectangle). It satisfies all properties of parallelograms, rhombuses, rectangles, and even itself! It's the most symmetrical quadrilateral.
-
Rectangle: A rectangle is a parallelogram with right angles. While its opposite sides are equal and parallel, its adjacent sides might have unequal lengths, distinguishing it from a rhombus.
Beyond the Basics: Advanced Properties
For a deeper understanding, let’s explore some more advanced properties:
-
Area Calculation:
- Parallelogram: Area = base × height. The height is the perpendicular distance between the parallel sides.
- Rhombus: Area = (1/2) × diagonal1 × diagonal2. The diagonals are the lines connecting opposite vertices.
-
Perimeter Calculation:
- Parallelogram: Perimeter = 2(side1 + side2).
- Rhombus: Perimeter = 4 × side (since all sides are equal).
-
Symmetry:
- Parallelogram: Has rotational symmetry of order 2 (180-degree rotation).
- Rhombus: Has rotational symmetry of order 2 (180-degree rotation) and two lines of reflectional symmetry.
Conclusion: Clear Distinctions, Shared Ancestry
While both parallelograms and rhombuses are quadrilaterals with parallel sides, the crucial difference lies in the lengths of their sides. A parallelogram simply requires opposite sides to be equal and parallel, while a rhombus mandates all four sides to be equal in length. This seemingly small difference leads to distinct geometric properties, particularly concerning the angles and diagonals. Understanding these nuances is key to mastering geometric concepts and appreciating the beauty and intricacy of shapes found in both mathematics and the real world. By understanding the core properties, advanced calculations, and practical applications, you can effectively utilize these geometric shapes in various fields.
Latest Posts
Latest Posts
-
How Many Germ Layers Do Porifera Have
May 12, 2025
-
What Is The Molar Mass Of Bromine
May 12, 2025
-
How Long Does It Take For A Capacitor To Discharge
May 12, 2025
-
Ph Of Vinegar And Baking Soda
May 12, 2025
-
Is Osmosis Low To High Or High To Low
May 12, 2025
Related Post
Thank you for visiting our website which covers about What Is The Difference Between A Rhombus And Parallelogram . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.