What Is Square Root Of 65
Juapaving
Apr 04, 2025 · 5 min read
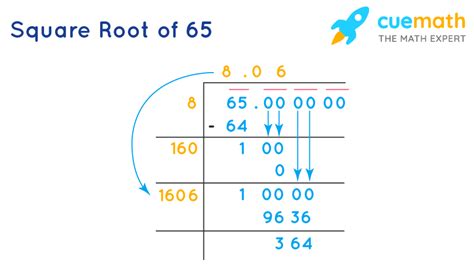
Table of Contents
What is the Square Root of 65? A Deep Dive into Irrational Numbers and Approximation Methods
The seemingly simple question, "What is the square root of 65?" opens a fascinating exploration into the world of mathematics, specifically irrational numbers and the various methods used to approximate their values. While a precise, finite decimal representation doesn't exist, understanding why and exploring different approaches to finding an approximate value is both educational and practically useful.
Understanding Square Roots and Irrational Numbers
Before delving into the specifics of √65, let's establish a foundational understanding. The square root of a number (x) is a value that, when multiplied by itself, equals x. In simpler terms, it's the number that, when squared, gives you the original number. For example, the square root of 9 (√9) is 3 because 3 * 3 = 9.
However, not all numbers have whole number square roots. Numbers like 65 fall into the category of irrational numbers. Irrational numbers are real numbers that cannot be expressed as a simple fraction (a ratio of two integers). Their decimal representation is non-terminating (it goes on forever) and non-repeating (it doesn't have a repeating pattern). This means we can only ever find an approximation of √65, not its exact value.
Methods for Approximating √65
Several methods exist for approximating the square root of 65. Let's explore some of the most common and effective ones:
1. Babylonian Method (or Heron's Method)
This iterative method is an ancient algorithm for approximating square roots. It refines an initial guess through successive calculations, converging towards the actual value. Here's how it works:
-
Start with an initial guess: Let's choose 8 as our initial guess because 8² = 64, which is close to 65.
-
Iterate using the formula: The formula for the Babylonian method is:
x_(n+1) = 0.5 * (x_n + (N / x_n))Where:
x_nis the current guess.Nis the number whose square root we're seeking (65 in this case).x_(n+1)is the improved guess.
-
Repeat: Substitute the new guess back into the formula and repeat the process until the desired level of accuracy is achieved.
Let's perform a few iterations:
- Iteration 1:
x_1 = 0.5 * (8 + (65 / 8)) ≈ 8.0625 - Iteration 2:
x_2 = 0.5 * (8.0625 + (65 / 8.0625)) ≈ 8.0622577 - Iteration 3:
x_3 = 0.5 * (8.0622577 + (65 / 8.0622577)) ≈ 8.0622577
As you can see, the value converges quickly. After just a few iterations, we have a highly accurate approximation of √65 ≈ 8.0622577.
2. Using a Calculator
Modern calculators have built-in functions to calculate square roots directly. This is the simplest and most practical method for finding an approximate value in everyday situations. Simply input √65 into your calculator, and it will provide a decimal approximation, usually to several decimal places.
3. Linear Approximation
This method uses the tangent line of the function f(x) = √x at a nearby point to estimate the value. While less precise than the Babylonian method, it's conceptually simpler.
Let's use the point x=64 (where √64 = 8). The derivative of √x is 1/(2√x). At x=64, the derivative is 1/(2*8) = 1/16.
The equation of the tangent line is:
y - 8 = (1/16)(x - 64)
Substituting x = 65:
y - 8 = (1/16)(1) y ≈ 8.0625
This provides a reasonable approximation, albeit less accurate than the Babylonian method.
4. Newton-Raphson Method
This is another iterative method, similar in spirit to the Babylonian method but with a more general approach applicable to various types of equations. It's based on finding the roots of a function using its derivative. For finding √65, we would consider the function f(x) = x² - 65 and iteratively refine an initial guess using the formula:
x_(n+1) = x_n - f(x_n) / f'(x_n)
where f'(x) is the derivative of f(x).
This method, while powerful, is more complex than the Babylonian method and may require more iterations for the same level of accuracy.
Why is √65 Irrational?
The proof that √65 is irrational relies on the concept of proof by contradiction. We assume √65 is rational, meaning it can be expressed as a fraction a/b where a and b are integers with no common factors (i.e., the fraction is in its simplest form).
-
Assume √65 is rational: √65 = a/b
-
Square both sides: 65 = a²/b²
-
Rearrange: 65b² = a²
-
Deduction: This implies that a² is a multiple of 65. Since 65 = 5 * 13, a² must be a multiple of both 5 and 13. Therefore, 'a' itself must be a multiple of both 5 and 13. We can express this as a = 5 * 13 * k (where k is an integer).
-
Substitute: Substitute a = 5 * 13 * k back into the equation 65b² = a²:
65b² = (5 * 13 * k)² 65b² = 65² * k² b² = 65k²
-
Deduction: This implies that b² is also a multiple of 65, and therefore 'b' must also be a multiple of both 5 and 13.
-
Contradiction: We've shown that both 'a' and 'b' are multiples of 5 and 13. This contradicts our initial assumption that a/b is in its simplest form (no common factors).
-
Conclusion: Our initial assumption that √65 is rational must be false. Therefore, √65 is irrational.
Practical Applications and Conclusion
While the exact value of √65 remains elusive, its approximation is crucial in various fields. Engineers, physicists, and computer scientists frequently encounter situations where calculating or approximating square roots is necessary. Applications range from calculating distances and areas in geometry to solving complex equations in physics and computer graphics.
Understanding different approximation methods, their strengths, and limitations provides a deeper appreciation for the nature of irrational numbers and the ingenuity of mathematical algorithms. The seemingly simple question of "What is the square root of 65?" leads to a rich exploration of mathematical concepts and practical techniques. Whether using a calculator for quick results or employing more sophisticated methods for greater precision, the ability to approximate irrational numbers like √65 remains a valuable skill in various fields. The choice of method depends on the desired level of accuracy and the available resources. The Babylonian method offers a balance of simplicity and accuracy, making it a widely applicable technique.
Latest Posts
Latest Posts
-
What Is Saponification In The Context Of Soap Making
Apr 10, 2025
-
What Is The Simplest Form Of 8 10
Apr 10, 2025
-
Which Of The Following Is Not Part Of Axial Skeleton
Apr 10, 2025
-
What Are All Of The Factors Of 39
Apr 10, 2025
-
What Are Some Factors Of 21
Apr 10, 2025
Related Post
Thank you for visiting our website which covers about What Is Square Root Of 65 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.