What Is Greater 1 3 Or 1 4
Juapaving
May 09, 2025 · 4 min read
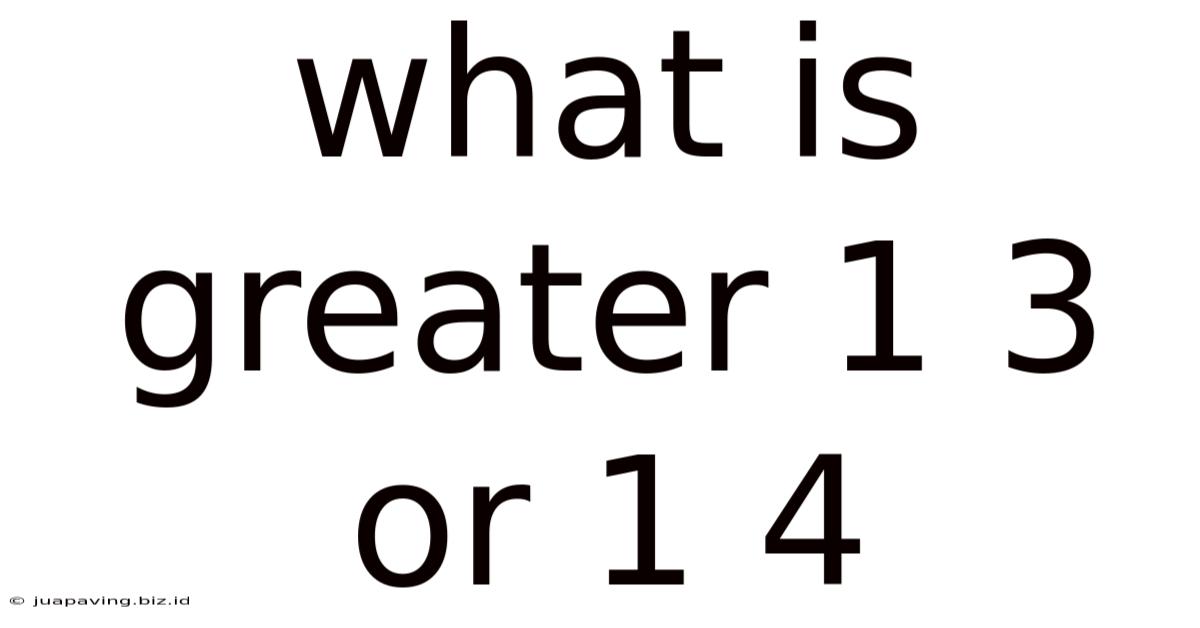
Table of Contents
What's Greater: 1/3 or 1/4? A Deep Dive into Fractions
Understanding fractions is fundamental to mathematics, forming the building blocks for more advanced concepts. While comparing simple fractions like 1/3 and 1/4 might seem trivial at first glance, it provides a valuable opportunity to solidify your understanding of fractional values and explore various methods for comparing them. This article delves into the comparison of 1/3 and 1/4, offering multiple approaches to determine which fraction is greater, and exploring the broader implications of understanding fraction comparisons.
Visualizing Fractions: The Pie Chart Approach
One of the most intuitive ways to grasp the concept of fractions is through visualization. Imagine two identical pies. We divide the first pie into three equal slices, representing 1/3. We divide the second pie into four equal slices, representing 1/4.
The Visual Comparison
Looking at the two pies, it's immediately apparent that each slice in the pie divided into three (1/3) is larger than each slice in the pie divided into four (1/4). This visual representation clearly demonstrates that 1/3 is greater than 1/4.
Numerical Comparison: Finding a Common Denominator
While the visual method is helpful for understanding, a more rigorous approach involves numerical comparison. This involves finding a common denominator for both fractions.
Understanding Denominators
The denominator (the bottom number in a fraction) represents the total number of equal parts a whole is divided into. The numerator (the top number) represents the number of those parts we are considering.
Finding the Least Common Multiple (LCM)
To compare 1/3 and 1/4, we need to find a common denominator. The easiest way is to find the least common multiple (LCM) of 3 and 4. The multiples of 3 are 3, 6, 9, 12, 15... and the multiples of 4 are 4, 8, 12, 16... The least common multiple is 12.
Converting to the Common Denominator
Now we convert both fractions to have a denominator of 12:
- 1/3: To get a denominator of 12, we multiply both the numerator and the denominator by 4: (1 x 4) / (3 x 4) = 4/12
- 1/4: To get a denominator of 12, we multiply both the numerator and the denominator by 3: (1 x 3) / (4 x 3) = 3/12
The Result
Now we have 4/12 and 3/12. Since both fractions have the same denominator, we can directly compare the numerators. Since 4 > 3, we can confidently conclude that 4/12 (or 1/3) is greater than 3/12 (or 1/4).
Decimal Conversion: A Different Perspective
Converting fractions to decimals provides another method for comparison.
Converting Fractions to Decimals
- 1/3: 1 ÷ 3 = 0.333... (a repeating decimal)
- 1/4: 1 ÷ 4 = 0.25
Comparing Decimals
Comparing 0.333... and 0.25 is straightforward. 0.333... is clearly greater than 0.25, reinforcing our previous findings.
The Significance of Understanding Fraction Comparison
The seemingly simple task of comparing 1/3 and 1/4 is crucial for building a strong foundation in mathematics. These skills are essential for:
- Solving Real-World Problems: From dividing recipes to calculating proportions in construction, understanding fractions is vital in everyday life.
- Advanced Mathematical Concepts: Fractions are fundamental to algebra, calculus, and numerous other advanced mathematical topics. A solid understanding of basic fraction comparison is essential for tackling these more complex concepts.
- Data Interpretation: Analyzing data often involves working with fractions and percentages, requiring a solid understanding of fractional values.
- Improving Problem-Solving Skills: Comparing fractions develops critical thinking and problem-solving skills, enhancing overall cognitive abilities.
Extending the Concept: Comparing More Complex Fractions
The principles discussed here can be extended to compare more complex fractions. The same methods—visual representation, finding a common denominator, and decimal conversion—can be applied to fractions with larger numerators and denominators.
Example: Comparing 5/8 and 3/5
Let's compare 5/8 and 3/5 using the common denominator method. The LCM of 8 and 5 is 40.
- 5/8: (5 x 5) / (8 x 5) = 25/40
- 3/5: (3 x 8) / (5 x 8) = 24/40
Since 25 > 24, 5/8 is greater than 3/5.
Conclusion: Mastering Fractions for a Brighter Future
The seemingly simple question, "What's greater: 1/3 or 1/4?" leads us to a deeper understanding of fractions and their significance in mathematics and beyond. Mastering fraction comparison techniques empowers individuals to approach more complex mathematical problems with confidence and clarity, paving the way for success in various academic and professional endeavors. From everyday applications to advanced mathematical concepts, the ability to compare fractions is a fundamental skill that serves as a building block for future learning and problem-solving. By consistently practicing these methods and understanding the underlying principles, you can confidently navigate the world of fractions and unlock a deeper appreciation for the power of mathematics. The ability to accurately and efficiently compare fractions is not just a mathematical skill; it’s a crucial component of critical thinking and problem-solving, applicable far beyond the classroom.
Latest Posts
Latest Posts
-
Difference Between Nadh And Nadph In Humans
May 10, 2025
-
The Quotient Of A Number And 4 Is
May 10, 2025
-
What Is An Example Of Longitudinal Wave
May 10, 2025
-
What Part Of The Cell Maintains Homeostasis
May 10, 2025
-
Can Displacement Be Greater Than Distance
May 10, 2025
Related Post
Thank you for visiting our website which covers about What Is Greater 1 3 Or 1 4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.