What Is Bigger 3/4 Or 1/2
Juapaving
May 11, 2025 · 6 min read
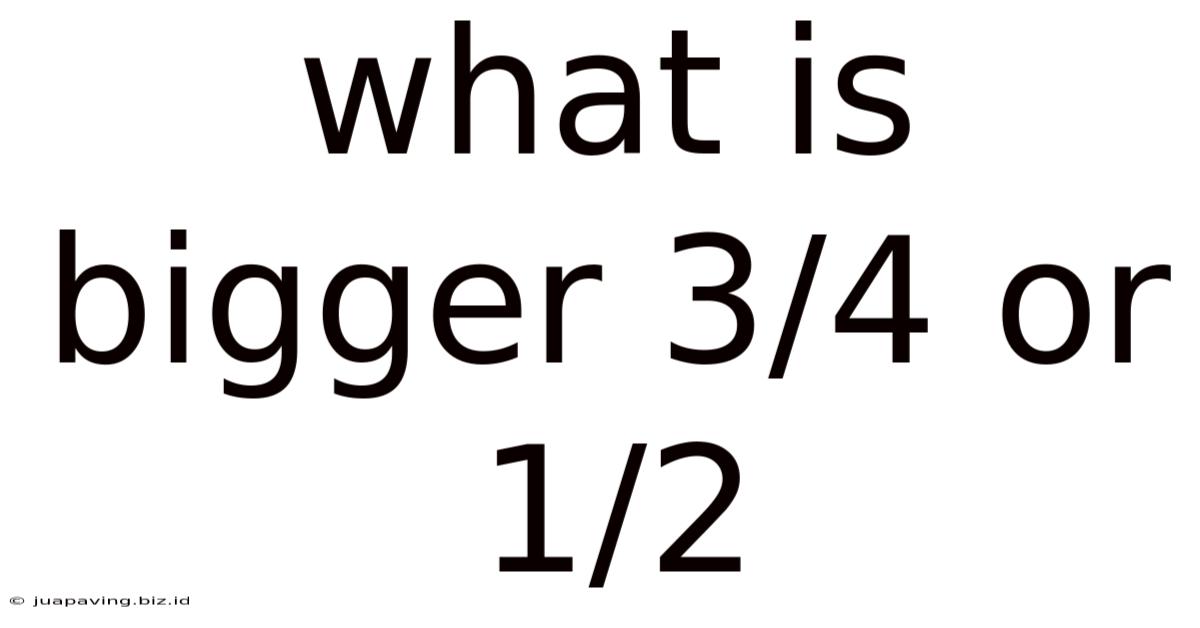
Table of Contents
What's Bigger: 3/4 or 1/2? A Deep Dive into Fractions
Determining which fraction is larger, 3/4 or 1/2, might seem like a simple task, especially for those comfortable with basic arithmetic. However, understanding the underlying principles behind comparing fractions is crucial for developing a strong foundation in mathematics and problem-solving. This article will not only answer the question definitively but also explore various methods for comparing fractions, providing you with the tools to tackle similar problems with confidence. We'll delve into visual representations, numerical comparisons, and even explore the practical applications of understanding fraction size.
Understanding Fractions: A Quick Refresher
Before we jump into comparing 3/4 and 1/2, let's refresh our understanding of what fractions represent. A fraction is a part of a whole. It's expressed as a ratio of two numbers: the numerator (the top number) and the denominator (the bottom number). The numerator indicates how many parts we have, while the denominator indicates how many equal parts the whole is divided into.
For example, in the fraction 3/4, the numerator (3) represents the number of parts we possess, and the denominator (4) indicates that the whole is divided into four equal parts. Similarly, in the fraction 1/2, we have one part out of two equal parts.
Visualizing the Comparison: The Power of Pictures
One of the simplest ways to compare fractions is through visual representation. Imagine a pizza.
Comparing with a Pizza
Let's consider two pizzas, both of the same size.
- Pizza 1: We cut this pizza into four equal slices. We eat three of those slices (3/4).
- Pizza 2: We cut this pizza into two equal slices. We eat one of those slices (1/2).
Which pizza had more eaten? Clearly, Pizza 1 (3/4) has a larger portion consumed than Pizza 2 (1/2). This visual representation clearly demonstrates that 3/4 is larger than 1/2.
Using Fraction Bars
Another visual aid is the use of fraction bars. Imagine two bars of equal length.
- Bar 1: Divide this bar into four equal parts and shade three of them (representing 3/4).
- Bar 2: Divide this bar into two equal parts and shade one of them (representing 1/2).
Visually comparing the shaded portions reinforces that 3/4 represents a larger area than 1/2.
Numerical Comparison Methods: Finding Common Ground
While visual representations are helpful, especially for beginners, we also need to master numerical methods for comparing fractions. These methods are essential when dealing with more complex fractions where visual aids become less practical.
Method 1: Finding a Common Denominator
The most common method involves finding a common denominator. A common denominator is a number that is a multiple of both denominators. In our case, we need a common denominator for 4 and 2. The smallest common denominator is 4 (since 2 x 2 = 4).
- Converting 1/2: To convert 1/2 to an equivalent fraction with a denominator of 4, we multiply both the numerator and the denominator by 2: (1 x 2) / (2 x 2) = 2/4.
Now we can easily compare 3/4 and 2/4. Since 3 > 2, we can definitively say that 3/4 > 1/2.
Method 2: Converting to Decimals
Another effective method involves converting the fractions into decimals. This method is particularly useful when comparing multiple fractions or when dealing with fractions that don't easily share a common denominator.
- Converting 3/4: To convert 3/4 to a decimal, we divide the numerator (3) by the denominator (4): 3 ÷ 4 = 0.75.
- Converting 1/2: To convert 1/2 to a decimal, we divide the numerator (1) by the denominator (2): 1 ÷ 2 = 0.5.
Comparing the decimal values, 0.75 > 0.5, confirms that 3/4 > 1/2.
Method 3: Cross-Multiplication (For Comparing Two Fractions)
Cross-multiplication provides a quick and efficient method for comparing two fractions. To compare a/b and c/d, we cross-multiply:
- Multiply a by d (a x d)
- Multiply b by c (b x c)
If (a x d) > (b x c), then a/b > c/d. If (a x d) < (b x c), then a/b < c/d.
Let's apply this to 3/4 and 1/2:
- (3 x 2) = 6
- (4 x 1) = 4
Since 6 > 4, we conclude that 3/4 > 1/2.
Practical Applications: Why Understanding Fractions Matters
Understanding how to compare fractions isn't just an academic exercise; it has numerous practical applications in everyday life.
Cooking and Baking
Recipes often involve fractions. Knowing which fraction is larger helps you understand the proportions of ingredients correctly. For instance, a recipe might call for 3/4 cup of flour and 1/2 cup of sugar. Understanding that 3/4 is larger than 1/2 helps you grasp the relative amounts of each ingredient.
Construction and Measurement
In construction and other trades, precise measurements are crucial. Comparing fractions ensures accurate measurements and prevents errors. For example, a carpenter might need to determine whether a 3/4-inch piece of wood is larger than a 1/2-inch piece.
Time Management
Time management often involves dealing with fractions of an hour or a day. Understanding fractions helps you schedule tasks and allocate time effectively. For example, you might have 3/4 of an hour to complete a task and need to assess if that's sufficient time.
Financial Calculations
Financial calculations often involve fractions, especially when dealing with percentages and interest rates. Understanding fractions is important for comprehending financial statements, budgeting, and making informed financial decisions.
Beyond the Basics: Extending Your Fraction Knowledge
Understanding the basics of comparing fractions is a stepping stone to more advanced concepts. Explore further by learning about:
- Improper fractions: Fractions where the numerator is greater than or equal to the denominator (e.g., 5/4).
- Mixed numbers: A combination of a whole number and a fraction (e.g., 1 1/4).
- Equivalent fractions: Fractions that represent the same value (e.g., 1/2 = 2/4 = 4/8).
- Adding, subtracting, multiplying, and dividing fractions: Mastering these operations expands your mathematical capabilities significantly.
Conclusion: Mastering Fractions for a Brighter Future
The question of whether 3/4 or 1/2 is larger is a seemingly simple one, yet it serves as a gateway to understanding the broader world of fractions. Mastering fraction comparison techniques – whether through visual aids or numerical methods – equips you with essential skills applicable to various aspects of life, from baking a cake to managing your finances. By embracing these methods and continually practicing, you'll build a strong foundation in mathematics and enhance your problem-solving abilities. Remember, the more you understand fractions, the better equipped you'll be to tackle more complex mathematical challenges in the future.
Latest Posts
Latest Posts
-
A Dna Nucleotide Is Composed Of
May 11, 2025
-
How Many Inches In 1 Cubic Feet
May 11, 2025
-
Animals That Are Active During The Day
May 11, 2025
-
Google Chrome Is An Example Of A
May 11, 2025
-
Cars A And B Are Travelling In The Same Direction
May 11, 2025
Related Post
Thank you for visiting our website which covers about What Is Bigger 3/4 Or 1/2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.