What Is A Factor Of 95
Juapaving
Mar 25, 2025 · 5 min read
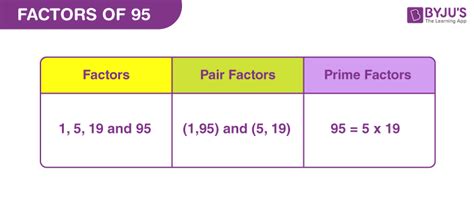
Table of Contents
What is a Factor of 95? A Deep Dive into Number Theory
Finding the factors of a number might seem like a simple arithmetic task, but it's a fundamental concept in number theory with far-reaching applications in mathematics and computer science. This article delves deep into the question: What is a factor of 95? We'll explore various methods for finding factors, discuss the properties of factors, and uncover the significance of this seemingly simple concept within the broader landscape of mathematics.
Understanding Factors
Before we tackle the specific case of 95, let's establish a clear definition of a factor. A factor (also known as a divisor) of a number is any integer that divides the number evenly, leaving no remainder. In other words, if a is a factor of b, then b divided by a results in a whole number.
For example, the factors of 12 are 1, 2, 3, 4, 6, and 12, because each of these numbers divides 12 evenly.
Methods for Finding Factors
Several methods can be used to identify the factors of a number. Let's examine some common approaches:
1. The Division Method
This is the most straightforward method. We systematically divide the number by each integer, starting from 1, and check if the result is a whole number. If it is, both the divisor and the quotient are factors. We continue this process until the divisor is equal to or greater than the square root of the number. Why the square root? Because once you pass the square root, you'll simply be repeating factors you've already found (in reverse order).
For 95, we would proceed as follows:
- 95 ÷ 1 = 95 (Factors: 1 and 95)
- 95 ÷ 5 = 19 (Factors: 5 and 19)
- The next number to try is 10 which is greater than the square root of 95 (approximately 9.75).
Therefore, the factors of 95 are 1, 5, 19, and 95.
2. Prime Factorization
Prime factorization is a powerful technique for finding all the factors of a number. It involves expressing the number as a product of its prime factors. A prime number is a whole number greater than 1 that has only two divisors: 1 and itself.
To prime factorize 95:
- We start by finding the smallest prime number that divides 95, which is 5.
- 95 ÷ 5 = 19. Since 19 is a prime number, we have found the prime factorization: 5 x 19.
Knowing the prime factorization allows us to systematically find all factors. We can combine the prime factors in various ways:
- 5<sup>0</sup> x 19<sup>0</sup> = 1
- 5<sup>1</sup> x 19<sup>0</sup> = 5
- 5<sup>0</sup> x 19<sup>1</sup> = 19
- 5<sup>1</sup> x 19<sup>1</sup> = 95
This method confirms that the factors of 95 are 1, 5, 19, and 95.
3. Factor Pairs
This method is particularly useful for smaller numbers. We look for pairs of numbers that multiply to give the target number.
For 95:
- 1 x 95 = 95
- 5 x 19 = 95
This gives us the factors 1, 5, 19, and 95.
Properties of Factors
Factors possess several interesting properties:
- 1 and the number itself are always factors. Every number is divisible by 1 and itself.
- The number of factors can vary. Some numbers have many factors (e.g., 12), while others have few (e.g., prime numbers only have two factors).
- Factors can be positive or negative. While we often focus on positive factors, -1, -5, -19, and -95 are also factors of 95 because they divide 95 evenly, resulting in a whole number.
- The product of factors: If a and b are factors of a number n, then their product, a * b, is also a factor of n.
Significance of Factors in Mathematics and Computer Science
The concept of factors underpins numerous mathematical and computational concepts:
- Greatest Common Divisor (GCD): The GCD of two numbers is the largest number that divides both evenly. Finding GCDs is crucial in simplifying fractions and solving various mathematical problems. Euclid's algorithm, a highly efficient method for finding GCDs, relies heavily on the concept of factors.
- Least Common Multiple (LCM): The LCM of two numbers is the smallest number that is a multiple of both. LCMs are essential in solving problems involving fractions and cycles.
- Modular Arithmetic: Modular arithmetic, used extensively in cryptography and computer science, is based on remainders after division. Understanding factors is crucial for grasping the principles of modular arithmetic.
- Polynomial Factoring: Factoring polynomials is a crucial technique in algebra and calculus, analogous to factoring integers. Understanding integer factors provides a foundation for grasping polynomial factoring.
- Cryptography: Prime factorization plays a fundamental role in many modern cryptographic systems, such as RSA encryption. The difficulty of factoring large numbers into their prime components is the basis for the security of these systems.
Conclusion: The Significance of Finding Factors of 95
While finding the factors of 95 might appear to be a simple exercise, it highlights the fundamental importance of factorisation in mathematics. This simple act of determining the divisors of a number opens doors to a deeper understanding of number theory and its applications in various fields. By mastering the methods discussed in this article, we can appreciate the elegance and power of factorisation, a concept that extends far beyond basic arithmetic. Understanding factors of a number like 95 is not just about finding numbers; it's about unlocking a world of mathematical possibilities. The seemingly simple question of "What is a factor of 95?" reveals a rich tapestry of mathematical concepts and their profound influence on the world around us. From the foundational concepts of prime factorization to the advanced applications in cryptography, the ability to find and analyze factors is an indispensable tool in any mathematician's or computer scientist's arsenal. Therefore, the ability to accurately and efficiently find factors is crucial for success in various fields. The next time you encounter a question about factors, remember the depth and breadth of this seemingly simple mathematical concept.
Latest Posts
Latest Posts
-
Barium Chloride Reacts With Sodium Sulfate
Mar 28, 2025
-
Tension Is Measured In What Units
Mar 28, 2025
-
What Is The Decimal For 7
Mar 28, 2025
-
Radius Of Convergence Power Series Calculator
Mar 28, 2025
-
Is Dna Copied Before Meiosis Ii
Mar 28, 2025
Related Post
Thank you for visiting our website which covers about What Is A Factor Of 95 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
