What Is 9 Percent Of 16
Juapaving
May 13, 2025 · 4 min read
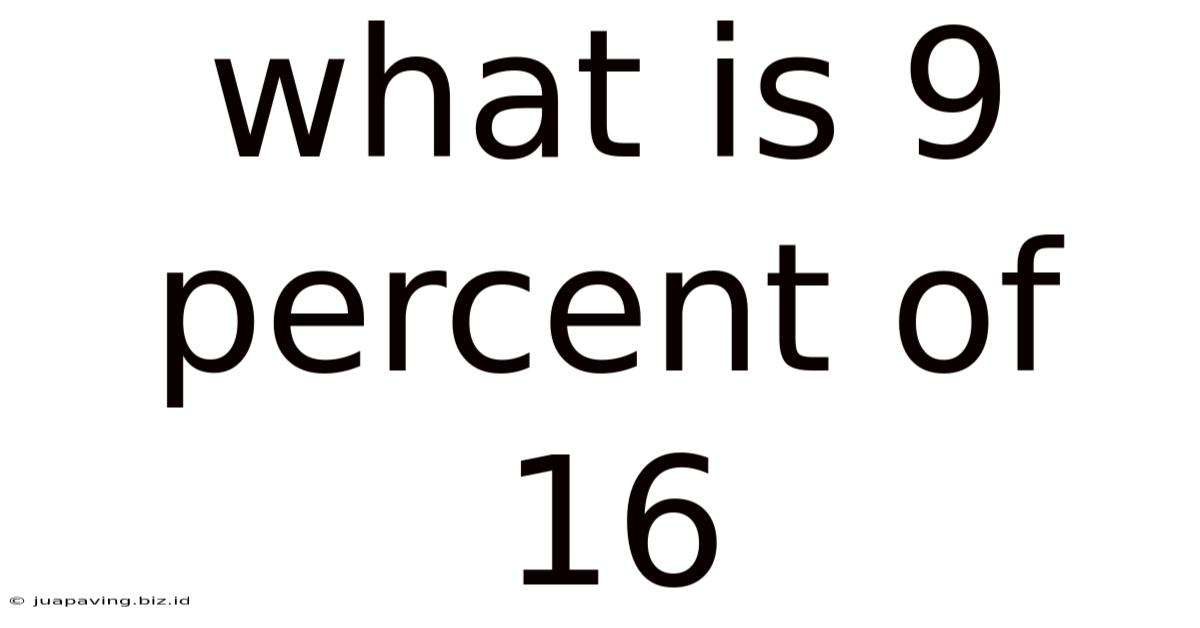
Table of Contents
What is 9 Percent of 16? A Deep Dive into Percentage Calculations
This seemingly simple question, "What is 9 percent of 16?", opens a door to a broader understanding of percentage calculations, their applications, and the underlying mathematical principles. While the answer itself is easily obtained with a calculator or a quick formula, exploring the how and why behind the calculation reveals valuable insights applicable to numerous real-world scenarios. This article delves into the various methods of solving this problem, explores the practical applications of percentage calculations, and offers strategies for tackling more complex percentage problems.
Understanding Percentages: The Foundation
Before diving into the specific calculation, let's establish a firm understanding of what a percentage represents. A percentage is simply a fraction expressed as a part of 100. The symbol "%" denotes "per hundred" or "out of 100". Therefore, 9% can be written as 9/100 or 0.09. This fundamental understanding is crucial for solving any percentage problem.
Method 1: The Direct Calculation Method
The most straightforward method to find 9% of 16 is to convert the percentage to a decimal and then multiply it by the number.
Steps:
- Convert the percentage to a decimal: 9% = 9/100 = 0.09
- Multiply the decimal by the number: 0.09 * 16 = 1.44
Therefore, 9% of 16 is 1.44.
This method is efficient and easily adaptable to various percentage calculations. It relies on the core understanding that a percentage is essentially a fraction of a whole.
Method 2: The Fraction Method
This method utilizes the fractional representation of percentages.
Steps:
- Express the percentage as a fraction: 9% = 9/100
- Multiply the fraction by the number: (9/100) * 16 = 144/100
- Simplify the fraction (if possible): 144/100 can be simplified to 36/25
- Convert the fraction to a decimal: 36/25 = 1.44
Again, the result is 1.44. This method reinforces the conceptual link between percentages, fractions, and decimals. It’s particularly helpful when dealing with percentages that can be easily expressed as simple fractions.
Method 3: Using Proportions
The proportion method provides a more visual and intuitive approach to solving percentage problems. It leverages the concept of equivalent ratios.
Steps:
- Set up a proportion: 9/100 = x/16, where 'x' represents 9% of 16.
- Cross-multiply: 9 * 16 = 100 * x
- Solve for x: 144 = 100x => x = 144/100 = 1.44
This method highlights the relationship between the parts and the whole, demonstrating the proportional equivalence involved in percentage calculations.
Real-World Applications of Percentage Calculations
Understanding percentage calculations is crucial in numerous everyday situations:
- Sales and Discounts: Calculating discounts on sale items. For example, a 20% discount on a $50 item.
- Taxes: Determining the amount of sales tax or income tax owed.
- Tips and Gratuities: Calculating appropriate tips at restaurants or for service providers.
- Interest Rates: Understanding interest earned on savings accounts or interest paid on loans.
- Financial Analysis: Analyzing financial statements, investment returns, and profit margins.
- Statistics and Data Analysis: Representing data as percentages to make it easier to understand and compare.
- Scientific Applications: Expressing experimental results or changes in quantities as percentages.
Tackling More Complex Percentage Problems
The fundamental principles discussed above can be extended to solve more complex percentage problems:
-
Finding the percentage increase or decrease: This involves calculating the difference between two values and expressing it as a percentage of the original value. For instance, calculating the percentage increase in sales from one year to the next.
-
Finding the original value: This requires working backwards from a percentage and a resulting value. For example, if a discounted price is $40 after a 25% discount, finding the original price.
-
Compound percentages: This involves calculating percentages repeatedly, often used in scenarios like compound interest calculations where interest is earned on both the principal amount and accumulated interest.
Practical Tips for Solving Percentage Problems
- Convert percentages to decimals or fractions: This simplifies calculations significantly.
- Use a calculator: For larger numbers or more complex calculations, a calculator can save time and increase accuracy.
- Check your work: Always double-check your calculations to ensure accuracy.
- Understand the context: Make sure you understand the question and what it's asking you to calculate.
- Practice regularly: The more you practice, the better you'll become at solving percentage problems.
Conclusion
While the answer to "What is 9 percent of 16?" is a simple 1.44, the journey to arrive at this answer reveals a wealth of knowledge about percentage calculations and their pervasive applications. By mastering these fundamental concepts and employing the various methods described above, you equip yourself with valuable skills applicable across numerous academic, professional, and everyday life scenarios. The ability to confidently tackle percentage problems translates to a deeper understanding of data, financial matters, and a wide array of quantitative information. Remember to practice regularly and explore the diverse applications of percentages to further solidify your understanding and build confidence in your mathematical abilities.
Latest Posts
Latest Posts
-
1 Base Pair How Many Nucleotides
May 13, 2025
-
5 Letter Words Beginning With A G
May 13, 2025
-
How Many Thousands Make A Crore
May 13, 2025
-
How Many Seconds Are In 4 Days
May 13, 2025
-
How To Find Percentage Abundance Of 3 Isotopes
May 13, 2025
Related Post
Thank you for visiting our website which covers about What Is 9 Percent Of 16 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.