What Is 8 5 As A Mixed Number
Juapaving
May 10, 2025 · 6 min read
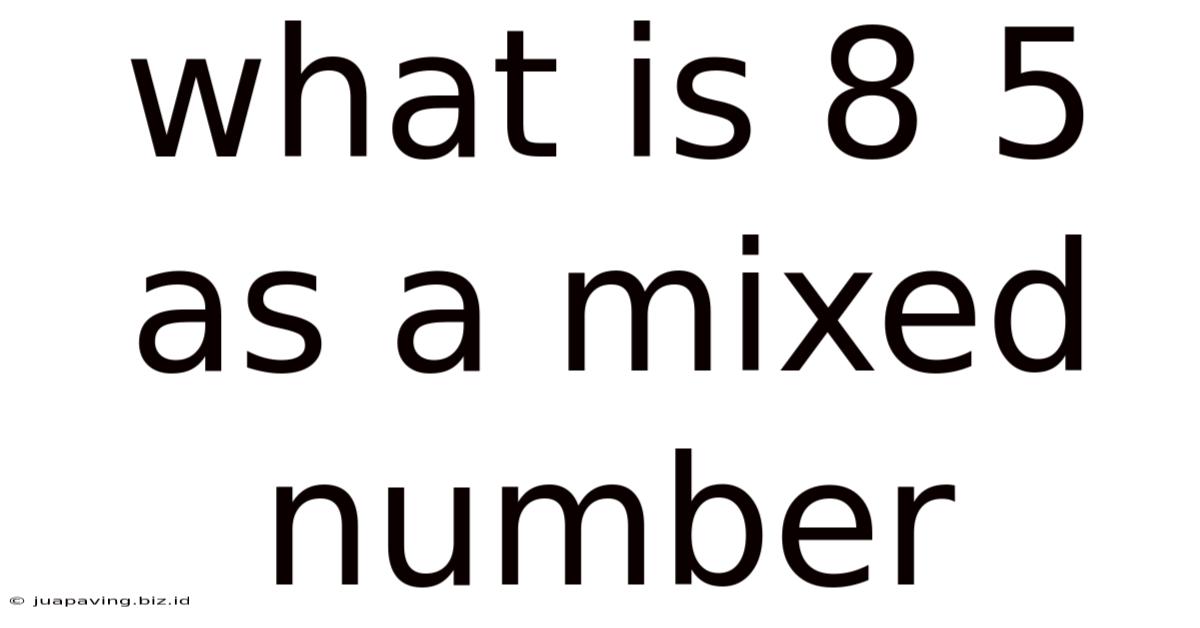
Table of Contents
What is 8/5 as a Mixed Number? A Comprehensive Guide
The question "What is 8/5 as a mixed number?" might seem simple at first glance, but it unlocks a deeper understanding of fractions and their representation. This comprehensive guide will not only answer this question but also explore the broader concept of converting improper fractions to mixed numbers, providing you with the tools and knowledge to tackle similar conversions with confidence. We'll cover various methods, practical applications, and even delve into the history behind this fundamental mathematical concept.
Understanding Fractions: A Quick Recap
Before diving into the conversion, let's refresh our understanding of fractions. A fraction represents a part of a whole. It consists of two main components:
- Numerator: The top number, indicating the number of parts we have.
- Denominator: The bottom number, indicating the total number of equal parts the whole is divided into.
In the fraction 8/5, 8 is the numerator and 5 is the denominator. This means we have 8 parts out of a possible 5 equal parts. This type of fraction, where the numerator is larger than the denominator, is called an improper fraction. Improper fractions represent a value greater than one.
Converting 8/5 to a Mixed Number: The Process
A mixed number combines a whole number and a proper fraction (a fraction where the numerator is smaller than the denominator). Converting an improper fraction like 8/5 to a mixed number involves determining how many whole units are contained within the fraction and representing the remaining part as a proper fraction.
Here's the step-by-step process:
-
Divide the Numerator by the Denominator: Divide 8 (the numerator) by 5 (the denominator). 8 ÷ 5 = 1 with a remainder of 3.
-
Identify the Whole Number: The quotient (the result of the division) becomes the whole number part of the mixed number. In this case, the whole number is 1.
-
Determine the Proper Fraction: The remainder (the number left over after the division) becomes the numerator of the proper fraction. The denominator remains the same as the original fraction's denominator. So, the remainder 3 becomes the numerator, and the denominator remains 5. This gives us the proper fraction 3/5.
-
Combine the Whole Number and Proper Fraction: Combine the whole number and the proper fraction to form the mixed number. Therefore, 8/5 as a mixed number is 1 3/5.
Visualizing the Conversion
Imagine you have 8 pizzas, each sliced into 5 equal pieces. You can take 5 of those slices to make a whole pizza. You'll have 1 whole pizza and 3 slices remaining (out of the 5 slices in a pizza). This visually represents the mixed number 1 3/5.
Alternative Methods for Conversion
While the long division method is the most common, there are alternative approaches to convert improper fractions to mixed numbers:
-
Subtracting the Denominator: Repeatedly subtract the denominator from the numerator until you reach a number smaller than the denominator. The number of times you subtract the denominator represents the whole number, and the remaining number becomes the numerator of the proper fraction. For 8/5: 8 - 5 = 3. We subtracted once, so the whole number is 1, and the remainder 3 becomes the numerator.
-
Using Multiplication and Subtraction: This method involves finding the largest multiple of the denominator that's less than or equal to the numerator. In this case, 5 x 1 = 5, and 5 x 2 = 10. Since 10 is greater than 8, we use 5 x 1 = 5. Subtract 5 from 8 (8 - 5 = 3). The result of the subtraction becomes the numerator, and the denominator stays the same, giving you 3/5. The number of times you multiplied the denominator (in this case 1) becomes the whole number. This gives us the mixed number 1 3/5.
Practical Applications of Mixed Numbers
Mixed numbers are frequently used in everyday life and across various fields:
-
Cooking and Baking: Recipes often call for amounts expressed as mixed numbers (e.g., 2 1/2 cups of flour).
-
Measurement: Measuring lengths, weights, and volumes often involves mixed numbers (e.g., 3 1/4 inches).
-
Construction and Engineering: Precise measurements in construction and engineering often rely on mixed numbers for accuracy.
-
Time: Expressing time involves using mixed numbers (e.g., 1 hour and 30 minutes, or 1 1/2 hours).
Converting Mixed Numbers Back to Improper Fractions
It's equally important to understand how to convert a mixed number back into an improper fraction. This involves the following steps:
-
Multiply the whole number by the denominator: Multiply the whole number by the denominator of the proper fraction. For 1 3/5, this is 1 x 5 = 5.
-
Add the numerator: Add the result from step 1 to the numerator of the proper fraction. 5 + 3 = 8.
-
Keep the denominator: The denominator remains the same.
-
Combine to form the improper fraction: The result from step 2 becomes the numerator, and the denominator remains unchanged. This gives us the improper fraction 8/5.
The Historical Context of Fractions and Mixed Numbers
The use of fractions and mixed numbers can be traced back to ancient civilizations. Evidence suggests that Egyptians used unit fractions (fractions with a numerator of 1) as early as 1800 BC. The Babylonians, around the same time, developed a sexagesimal system (base-60) which influenced our modern system of measuring angles and time. The Greeks further developed the concept of fractions, and the Romans also contributed to their use. Over centuries, mathematicians refined the understanding and notation of fractions and mixed numbers, leading to the standard representation we use today.
Mastering Fraction Conversions: Tips and Tricks
-
Practice Regularly: Consistent practice is key to mastering fraction conversions. Try different examples and challenge yourself with more complex numbers.
-
Understand the Concept: Focus on understanding the underlying principles rather than just memorizing formulas. Visualizing the fraction can help.
-
Use Different Methods: Try the different methods discussed above to find the approach that best suits your learning style.
-
Check Your Work: Always verify your answer by converting the mixed number back to an improper fraction to ensure accuracy.
-
Utilize Online Resources: Numerous online tools and resources are available to aid in practice and understanding fraction conversions.
Conclusion: Beyond the Basics of 8/5
This in-depth guide has explored the conversion of the improper fraction 8/5 into the mixed number 1 3/5. We've examined various methods, highlighted practical applications, and delved into the historical context of this fundamental mathematical concept. By mastering fraction conversions, you'll enhance your mathematical skills and improve your ability to tackle a wide range of problems across various fields. Remember that consistent practice and a solid understanding of the underlying principles are crucial to success in working with fractions and mixed numbers. So, keep practicing, and you'll soon be confidently converting fractions with ease!
Latest Posts
Latest Posts
-
If Events A And B Are Mutually Exclusive Then
May 10, 2025
-
Which Of The Following Numbers Are Prime
May 10, 2025
-
Cell Wall Is Found In A Plant Or Animal
May 10, 2025
-
The Microscopic Study Of Tissues Is Called
May 10, 2025
-
Why Is The Vacuole Bigger In A Plant Cell
May 10, 2025
Related Post
Thank you for visiting our website which covers about What Is 8 5 As A Mixed Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.