What Is 8/3 As A Percent
Juapaving
May 13, 2025 · 4 min read
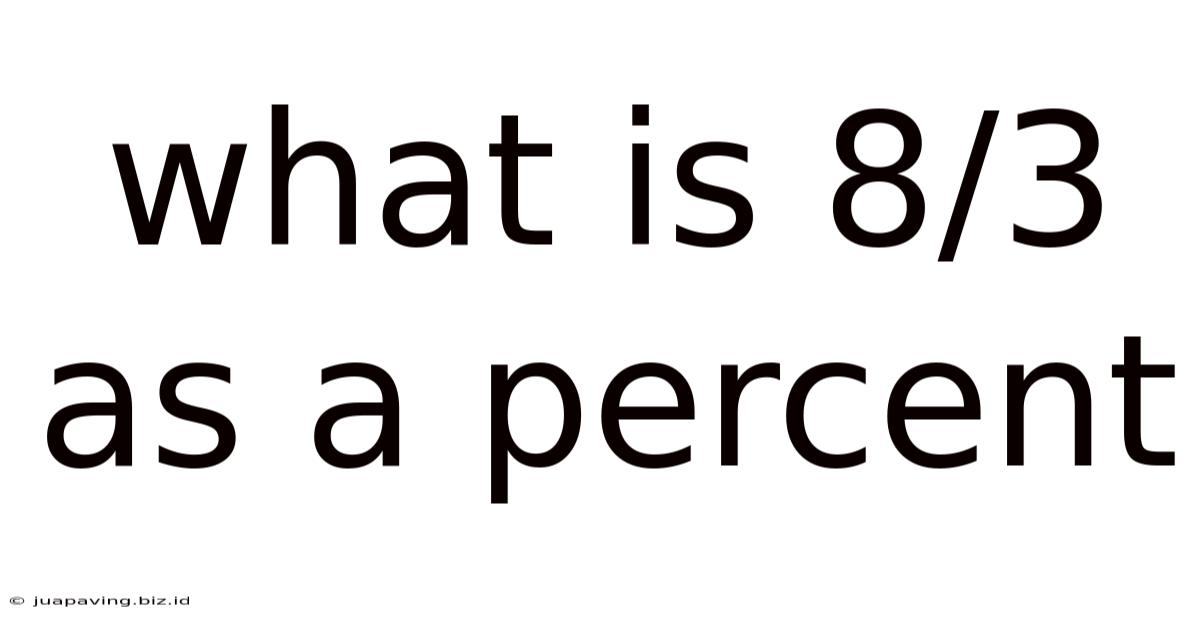
Table of Contents
What is 8/3 as a Percent? A Comprehensive Guide to Fraction-to-Percentage Conversions
Converting fractions to percentages is a fundamental skill in mathematics with applications across numerous fields, from finance and statistics to everyday life. Understanding this process is crucial for interpreting data, making comparisons, and solving problems effectively. This comprehensive guide will delve into the conversion of 8/3 to a percentage, explaining the methodology step-by-step and exploring related concepts to solidify your understanding.
Understanding Fractions and Percentages
Before diving into the conversion, let's briefly review the definitions of fractions and percentages.
Fractions: A fraction represents a part of a whole. It consists of two numbers: the numerator (the top number) and the denominator (the bottom number). The numerator indicates how many parts are being considered, while the denominator indicates the total number of equal parts the whole is divided into. For example, in the fraction 8/3, 8 is the numerator and 3 is the denominator.
Percentages: A percentage represents a fraction out of 100. The symbol "%" signifies "per hundred." Percentages are widely used to express proportions, rates, and changes. For instance, 50% means 50 out of 100, or one-half.
Converting 8/3 to a Percentage: The Step-by-Step Process
The conversion of a fraction to a percentage involves two primary steps:
Step 1: Convert the fraction to a decimal.
To convert a fraction to a decimal, divide the numerator by the denominator. In the case of 8/3:
8 ÷ 3 = 2.666666...
This decimal is a repeating decimal, indicated by the ellipsis (...). We'll address the handling of repeating decimals later.
Step 2: Convert the decimal to a percentage.
To convert a decimal to a percentage, multiply the decimal by 100 and add the percentage symbol (%).
2.666666... × 100 = 266.6666...%
Therefore, 8/3 is approximately 266.67%. We typically round to two decimal places for practical purposes.
Handling Repeating Decimals
As we saw, the decimal representation of 8/3 is a repeating decimal. Repeating decimals can be expressed in different ways:
-
Rounded decimal: Rounding to a specific number of decimal places provides an approximation. As shown above, rounding to two decimal places gives us 266.67%.
-
Using a bar notation: A bar above the repeating digits indicates the repetition. For 8/3, we could write 2.6̅, where the bar above the 6 signifies that the 6 repeats infinitely. This notation is more precise than rounding but may not be as practical for everyday use.
-
Expressing as a mixed number: We can also express the improper fraction 8/3 as a mixed number: 2 2/3. This representation doesn't directly give us a percentage, but it provides another way to understand the magnitude of the fraction.
Why is 8/3 greater than 100%?
It's important to note that 8/3 represents a value greater than 1. This is because the numerator (8) is larger than the denominator (3). When a fraction is greater than 1, its percentage equivalent will be greater than 100%. This simply means that the fraction represents more than a whole.
Real-World Applications of Fraction-to-Percentage Conversions
The ability to convert fractions to percentages is essential in various real-world scenarios:
-
Finance: Calculating interest rates, profit margins, and discounts often involves converting fractions to percentages. For example, an investment that yields 8/3 times the initial amount would represent a profit exceeding 166%.
-
Statistics: Representing data and probabilities frequently uses percentages. For example, if 8 out of 3 survey participants preferred a specific product, this could be expressed as approximately 266.67%—meaning the preference is significantly higher than the number of participants. (Note: While percentages exceeding 100% are valid mathematically, their interpretation in this specific context requires careful consideration. It's vital to clarify the meaning based on the data source.)
-
Everyday Life: Calculating tips, sales tax, and proportions in cooking and baking all rely on understanding percentage conversions.
Further Exploring Fraction-to-Percentage Conversions
To enhance your understanding of fraction-to-percentage conversions, consider exploring these related topics:
-
Converting mixed numbers to percentages: This involves first converting the mixed number to an improper fraction, and then following the steps outlined above.
-
Converting percentages to fractions: This is the reverse process of the conversion we've discussed. It involves dividing the percentage by 100 and simplifying the resulting fraction.
-
Using calculators and software for conversions: Many calculators and software programs have built-in functions for converting fractions to percentages and vice-versa, which can be particularly helpful when dealing with complex fractions or large numbers.
Conclusion: Mastering Fraction-to-Percentage Conversions
Converting fractions to percentages is a practical skill applicable across numerous domains. Mastering this skill not only enhances your mathematical proficiency but also equips you with the tools to analyze data effectively and confidently navigate various real-world scenarios. Remember the key steps: divide the numerator by the denominator to obtain the decimal, then multiply by 100 to express the result as a percentage. Pay close attention to repeating decimals and ensure appropriate rounding for practical applications. By understanding the underlying concepts and practicing consistently, you can build a solid foundation in working with fractions and percentages. This skill will prove invaluable in your academic pursuits and future endeavors.
Latest Posts
Latest Posts
-
How Many Square Meters In A Mile
May 13, 2025
-
Mountainous Region Between Black And Caspian Seas
May 13, 2025
-
What Do You Mean By Contra Entry
May 13, 2025
-
Which Statement Is Not True About A Heart Valve
May 13, 2025
-
A Mixture Of Sugar And Water Is A
May 13, 2025
Related Post
Thank you for visiting our website which covers about What Is 8/3 As A Percent . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.