What Is 60 Percent Of 2000
Juapaving
May 12, 2025 · 5 min read
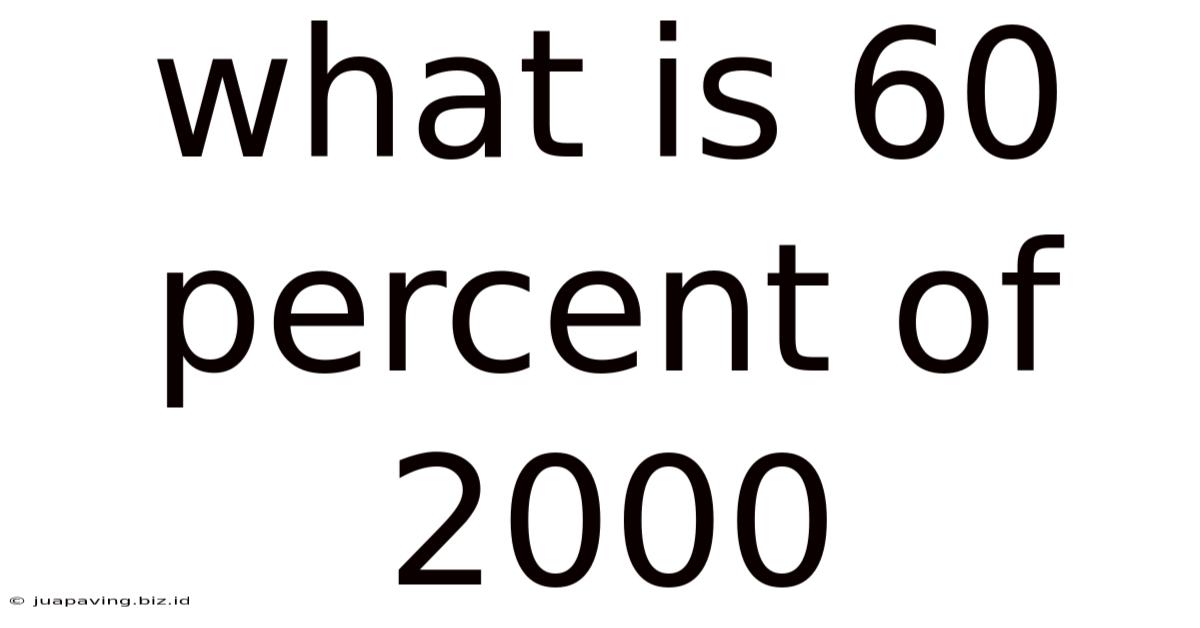
Table of Contents
What is 60 Percent of 2000? A Comprehensive Guide to Percentages and Their Applications
Calculating percentages is a fundamental skill with widespread applications in various aspects of life, from everyday finances to complex business analyses. Understanding how to determine percentages allows you to make informed decisions, analyze data effectively, and navigate numerical information confidently. This article delves into the question, "What is 60 percent of 2000?" providing not only the answer but also a comprehensive exploration of the underlying concepts, diverse applications, and practical methods for calculating percentages.
Understanding Percentages: A Fundamental Concept
A percentage is a fraction or ratio expressed as a number out of 100. The symbol "%" represents "percent," meaning "per hundred." Essentially, a percentage indicates a portion or proportion of a whole. For example, 60% means 60 out of 100, which can also be represented as the fraction 60/100 or the decimal 0.6.
This fundamental understanding forms the bedrock for all percentage calculations. Grasping this concept allows us to translate percentage problems into mathematical equations that can be easily solved.
Calculating 60 Percent of 2000: Methods and Approaches
There are several ways to calculate 60 percent of 2000. Let's explore the most common methods:
Method 1: Using the Decimal Equivalent
This is perhaps the most straightforward method. We convert the percentage to its decimal equivalent by dividing by 100. 60% becomes 0.60 (or simply 0.6). Then, we multiply this decimal by the number we're interested in, which is 2000:
0.6 * 2000 = 1200
Therefore, 60 percent of 2000 is 1200.
Method 2: Using Fractions
We can express 60% as a fraction: 60/100. This fraction simplifies to 3/5. Then, we multiply this fraction by 2000:
(3/5) * 2000 = 1200
Again, we arrive at the same answer: 60 percent of 2000 is 1200.
Method 3: Using Proportions
This method is particularly helpful for understanding the relationship between percentages and the whole. We set up a proportion:
x/2000 = 60/100
To solve for x (60% of 2000), we cross-multiply:
100x = 60 * 2000
100x = 120000
x = 120000/100
x = 1200
This confirms our previous calculations: 60 percent of 2000 is 1200.
Practical Applications of Percentage Calculations
The ability to calculate percentages has numerous practical applications in various fields:
Finance and Budgeting:
- Interest Calculations: Understanding interest rates is crucial for managing loans, savings accounts, and investments. Percentage calculations determine the amount of interest earned or paid.
- Discounts and Sales: Retail stores frequently offer discounts expressed as percentages. Calculating the discount amount and the final price requires understanding percentage calculations.
- Tax Calculations: Income tax, sales tax, and other taxes are usually expressed as percentages of the taxable amount. Accurate percentage calculations ensure correct tax payments.
- Investment Returns: Investors track their investment performance using percentages to measure gains or losses relative to the initial investment.
- Budgeting: Allocating a specific percentage of income to different budget categories (e.g., housing, food, transportation) helps in effective financial planning.
Business and Economics:
- Profit Margins: Businesses calculate profit margins as a percentage of sales revenue to assess profitability.
- Market Share: Companies analyze their market share as a percentage of the total market size to understand their competitive position.
- Growth Rates: Economic growth, sales growth, and other growth indicators are often expressed as percentages to show the rate of change over time.
- Inflation Rates: Inflation, the rate at which prices increase, is usually expressed as a percentage.
- Cost-Benefit Analysis: Businesses use percentage calculations in cost-benefit analysis to evaluate the financial feasibility of projects.
Science and Statistics:
- Data Analysis: Percentages are used extensively in statistical analysis to represent proportions and frequencies within datasets.
- Experimental Results: Scientists often express experimental results as percentages to indicate the success rate or the proportion of subjects exhibiting a specific characteristic.
- Probability: Percentages are used to represent probabilities in various contexts. For example, the probability of an event occurring can be expressed as a percentage.
Everyday Life:
- Tip Calculations: Calculating tips in restaurants often involves determining a specific percentage of the bill.
- Recipe Scaling: Adjusting recipe quantities often requires scaling ingredients proportionally, using percentages.
- Sales Tax Calculations: Knowing how to calculate sales tax is essential for budgeting and shopping.
- Understanding Surveys and Polls: Interpreting survey results and polls often requires understanding percentages and their significance.
Advanced Percentage Calculations: Beyond the Basics
While calculating 60% of 2000 is a relatively straightforward process, more complex scenarios may involve:
- Calculating percentage increase or decrease: These calculations require finding the difference between two values and expressing it as a percentage of the original value.
- Finding the original value given a percentage and the resulting value: This involves working backward from the result to find the initial amount.
- Compound percentages: These calculations involve applying percentages repeatedly over time, as is often the case with interest calculations.
- Percentage points vs. percentage change: It's essential to understand the distinction between these two concepts to avoid misinterpretations. A percentage point refers to an absolute change in percentage, whereas a percentage change refers to a relative change.
Mastering Percentage Calculations: Tips and Practice
Mastering percentage calculations takes practice. Here are some tips:
- Practice regularly: The more you practice, the more comfortable you'll become with different methods and applications.
- Use multiple methods: Try solving the same problem using different methods to enhance your understanding and identify the most efficient approach.
- Check your work: Always verify your answers to ensure accuracy. You can use online calculators or cross-check your calculations with alternative methods.
- Understand the context: Pay close attention to the specific context of the problem to avoid misinterpretations.
- Break down complex problems: Complex percentage problems can often be broken down into smaller, more manageable steps.
Conclusion: The Power of Percentages in a Data-Driven World
The ability to calculate percentages is a crucial skill in today's data-driven world. From managing personal finances to making informed business decisions, understanding percentages empowers you to navigate numerical information with confidence and make sound judgments. This article has explored the fundamental concepts of percentages, provided multiple methods for calculating 60% of 2000, and highlighted the diverse applications of percentage calculations across various fields. By mastering this skill, you equip yourself with a valuable tool for success in numerous aspects of life. Remember, consistent practice and a thorough understanding of the underlying principles are key to mastering this essential skill.
Latest Posts
Latest Posts
-
What Is The Length Of Rounded To The Nearest Tenth
May 12, 2025
-
What Is A Unit Of Electricity
May 12, 2025
-
Is Water A Pure Substance Or A Mixture
May 12, 2025
-
How Many Feet In 128 Inches
May 12, 2025
-
How Many Sides Do A Quadrilateral Have
May 12, 2025
Related Post
Thank you for visiting our website which covers about What Is 60 Percent Of 2000 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.