What Is 50 As A Percent
Juapaving
May 11, 2025 · 4 min read
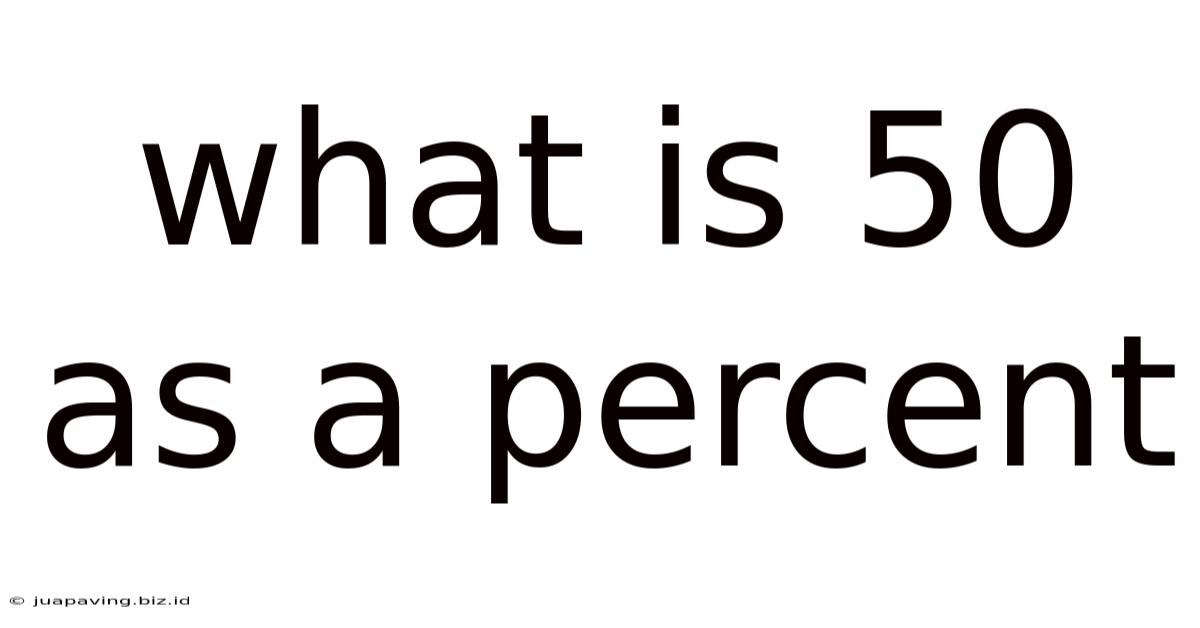
Table of Contents
What is 50 as a Percent? A Comprehensive Guide
Understanding percentages is a fundamental skill in various aspects of life, from calculating discounts and taxes to analyzing data and understanding financial reports. This comprehensive guide delves into the question: "What is 50 as a percent?" We will explore not just the simple answer but also the broader context of percentage calculations, providing you with a solid foundation to confidently tackle percentage-related problems.
The Simple Answer: 50 is 50%
The most straightforward answer is that 50 is 50% of 100. This is because a percentage represents a fraction out of 100. The number 50 represents 50 parts out of a total of 100 parts. Therefore, the percentage equivalent is 50%.
Understanding Percentages: A Deeper Dive
Before we delve into more complex scenarios, let's solidify our understanding of percentages. A percentage is a way of expressing a number as a fraction of 100. The word "percent" literally means "out of one hundred" (per cent). Therefore, any percentage can be represented as a fraction with a denominator of 100.
For instance:
- 25% can be written as 25/100, which simplifies to 1/4.
- 75% can be written as 75/100, which simplifies to 3/4.
- 50% can be written as 50/100, which simplifies to 1/2 or 0.5.
This fractional representation is crucial for understanding and performing calculations with percentages.
Calculating Percentages: Different Scenarios
While 50 as a percentage of 100 is straightforward, let's explore scenarios where the total isn't 100. This requires a slightly different approach.
Scenario 1: Finding the Percentage of a Number
Let's say you want to find out what percentage 50 represents of a different number, say 200. The formula to use is:
(Part / Whole) x 100 = Percentage
In this case:
(50 / 200) x 100 = 25%
Therefore, 50 is 25% of 200.
Scenario 2: Finding a Percentage of a Number
Conversely, you might need to find what number represents a specific percentage of another number. For example, what is 50% of 150? The formula here is:
(Percentage / 100) x Whole = Part
In this case:
(50 / 100) x 150 = 75
Therefore, 50% of 150 is 75.
Scenario 3: Finding the Whole when given a Part and Percentage
Imagine you know that 50 represents 20% of a certain number. How do you find the whole number? Rearrange the formula:
Whole = (Part / Percentage) x 100
In this instance:
Whole = (50 / 20) x 100 = 250
Therefore, 50 is 20% of 250.
Real-World Applications of Percentage Calculations
Understanding percentages is vital in many real-world applications:
- Sales and Discounts: Calculating discounts on sale items. A 50% off sale means you pay half the original price.
- Taxes: Determining the amount of tax payable on goods and services.
- Finance: Calculating interest rates, returns on investments, and loan repayments.
- Statistics: Analyzing data sets, understanding proportions, and interpreting surveys.
- Everyday Life: Dividing bills, calculating tips, and understanding proportions in recipes.
Tips and Tricks for Working with Percentages
- Memorize common percentages: Learning the fractional equivalents of common percentages (like 25%, 50%, 75%) can greatly speed up calculations.
- Use a calculator: For complex calculations, a calculator is a valuable tool. Many calculators have a percentage function.
- Break down complex problems: If faced with a complex percentage problem, break it down into smaller, manageable steps.
- Check your work: Always double-check your calculations to ensure accuracy.
- Practice regularly: The more you practice, the more comfortable and proficient you'll become with percentage calculations.
Advanced Percentage Concepts
While the basic concepts are straightforward, understanding more advanced percentage concepts enhances your ability to work with complex data.
Percentage Change
This refers to the change in a value expressed as a percentage of the original value. The formula is:
[(New Value - Old Value) / Old Value] x 100 = Percentage Change
A positive result indicates an increase, while a negative result indicates a decrease.
Percentage Point Difference
This refers to the difference between two percentages. For example, if the interest rate increases from 5% to 10%, the percentage point difference is 5 percentage points (not 100%).
Conclusion: Mastering Percentages
Understanding what 50 represents as a percent – 50% of 100 – is just the starting point. This guide has provided a comprehensive exploration of percentages, covering fundamental concepts, practical applications, and advanced topics. By mastering these concepts, you’ll be equipped to confidently tackle various percentage-related problems in your personal and professional life. Remember to practice regularly and use the tips provided to refine your skills. With consistent effort, percentage calculations will become second nature, allowing you to analyze data, make informed decisions, and navigate numerical situations with greater ease and confidence. The ability to accurately and efficiently calculate percentages is a valuable asset that enhances your problem-solving capabilities and broadens your understanding of the numerical world around you. So, continue practicing and expand your knowledge to fully harness the power of percentages.
Latest Posts
Latest Posts
-
Do Prokaryotes Reproduce Sexually Or Asexually
May 13, 2025
-
What Is The Conjugate Base Of Ammonia
May 13, 2025
-
Cell Organelles And Their Functions Worksheet Answers
May 13, 2025
-
What Are The Prime Factors Of 77
May 13, 2025
-
5 Letter Word Starts With R Ends With E
May 13, 2025
Related Post
Thank you for visiting our website which covers about What Is 50 As A Percent . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.