What Is -3x + 1 Subtracted From 3x - 1
Juapaving
May 09, 2025 · 4 min read
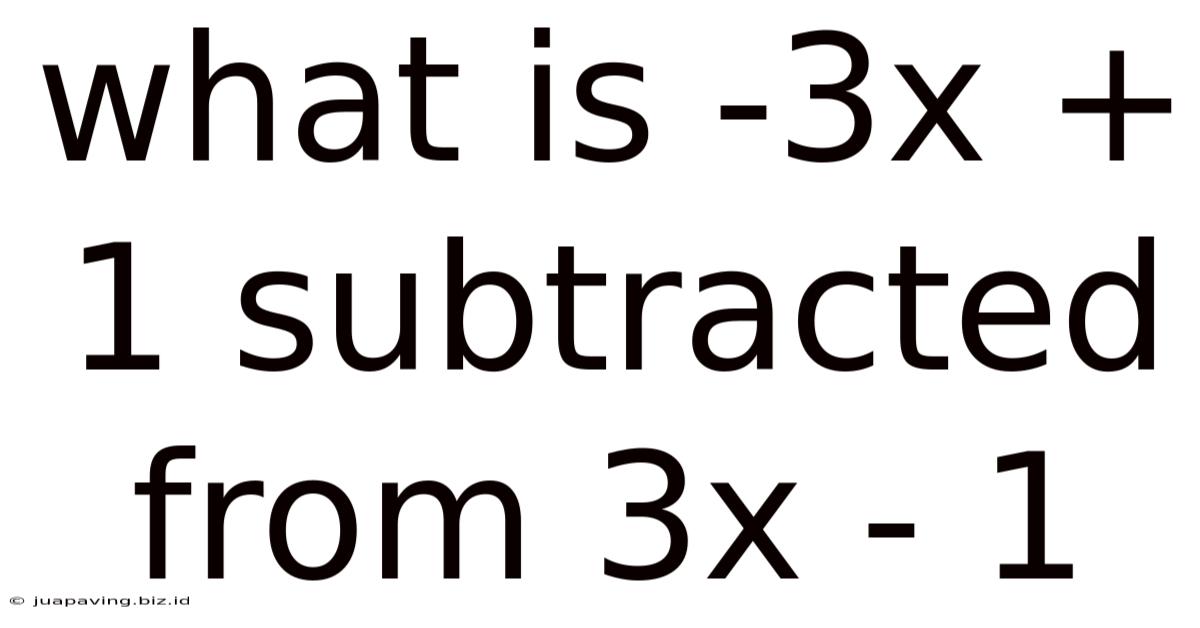
Table of Contents
What is 3x - 1 Subtracted from 3x - 1? A Deep Dive into Algebraic Subtraction
This seemingly simple subtraction problem, "What is 3x - 1 subtracted from 3x - 1?", opens a door to understanding fundamental algebraic concepts. While the immediate answer might seem obvious to some, a thorough exploration reveals valuable insights into simplifying expressions, the significance of parentheses, and the application of these principles in more complex algebraic scenarios. Let's unravel this problem step-by-step, exploring its nuances and broadening our algebraic understanding.
Understanding the Problem Statement
Before diving into the solution, it's crucial to accurately interpret the problem statement. The phrase "3x - 1 subtracted from 3x - 1" translates to the following algebraic expression:
(3x - 1) - (3x - 1)
Notice the use of parentheses. These are essential to indicate that we are subtracting the entire expression (3x - 1), not just a part of it. Ignoring the parentheses can lead to incorrect results.
Step-by-Step Solution
To solve this algebraic subtraction, we'll follow these steps:
Step 1: Distribute the Negative Sign
The minus sign before the second parenthesis acts as a -1 multiplier. We need to distribute this -1 to each term inside the second parenthesis:
(3x - 1) + (-1)(3x - 1)
This simplifies to:
(3x - 1) + (-3x + 1)
Step 2: Combine Like Terms
Now, we group like terms together. "Like terms" are terms that have the same variable raised to the same power. In this case, we have 3x and -3x, and -1 and 1. Combining them gives us:
(3x - 3x) + (-1 + 1)
Step 3: Simplify the Expression
Simplifying the expression gives us:
0x + 0
Which further simplifies to:
0
Therefore, the result of subtracting (3x - 1) from (3x - 1) is 0.
Exploring the Implications: Beyond the Obvious
While the numerical answer is straightforward, this problem provides a valuable opportunity to reinforce several crucial algebraic concepts.
The Significance of Parentheses
The correct use of parentheses is paramount in algebraic manipulation. Parentheses establish order of operations and ensure that we are performing the intended mathematical actions. In our problem, omitting the parentheses would lead to an entirely different, and incorrect, result:
3x - 1 - 3x - 1 = -2 (Incorrect)
This highlights the importance of carefully considering the context and applying parentheses correctly.
Understanding Additive Inverses
The problem subtly introduces the concept of additive inverses. An additive inverse of a number is a number that, when added to it, results in zero. In our case, (3x - 1) and -(3x - 1) are additive inverses of each other. Their sum is zero, leading to the final solution.
Applications in More Complex Scenarios
The principles illustrated in this seemingly simple problem are fundamental to solving more complex algebraic expressions and equations. Consider the following examples:
(5x² + 2x - 7) - (5x² - 3x + 2)
Following the same steps as before:
- Distribute the negative sign: (5x² + 2x - 7) + (-5x² + 3x - 2)
- Combine like terms: (5x² - 5x²) + (2x + 3x) + (-7 - 2)
- Simplify: 0x² + 5x - 9 = 5x - 9
This example demonstrates how the same principles of distributing the negative sign and combining like terms are applicable to more complex polynomial expressions.
(3x - 1) / (3x - 1)
This example introduces a different type of problem. Here, we are dealing with division. Note that division by zero is undefined. Hence, solving this requires caution. If 3x - 1 ≠ 0, the answer is 1, but if 3x-1 =0 then the equation is undefined. This is an important consideration in algebraic manipulation as it deals with finding the domain of the function.
Expanding the Understanding: Real-World Applications
Algebraic subtraction, as illustrated by this problem, isn't confined to theoretical exercises. It has numerous real-world applications. Consider scenarios such as:
- Calculating profit and loss: Subtracting costs from revenue to determine profit.
- Determining net worth: Subtracting liabilities from assets to find net worth.
- Engineering and Physics: Calculating net force by subtracting opposing forces.
- Financial Modeling: Analyzing financial statements and forecasting future performance.
Conclusion: The Power of Simplicity
The seemingly trivial problem, "What is 3x - 1 subtracted from 3x - 1?", offers a powerful lesson in the foundational principles of algebra. Through careful analysis and application of basic algebraic rules, we can easily arrive at the solution and, more importantly, gain a deeper understanding of the underlying concepts. Mastering these fundamentals provides a strong base for tackling more intricate algebraic problems and applying them to various real-world situations. Remember the importance of parentheses, the process of distributing negative signs, and the power of combining like terms—these are the cornerstones of algebraic success. The simplicity of this problem shouldn't be underestimated; it is a stepping stone to a much broader and more profound mathematical comprehension. Keep practicing, and your algebraic skills will surely flourish.
Latest Posts
Latest Posts
-
Kinetic Energy Of Simple Harmonic Motion
May 10, 2025
-
Which Of The Following Compounds Contains An Ionic Bond
May 10, 2025
-
Find The Limit Of Trigonometric Functions
May 10, 2025
-
Instruments That Produce Sound From A Vibrating String Are Called
May 10, 2025
-
How Many Grams Are In 0 50 Kilograms
May 10, 2025
Related Post
Thank you for visiting our website which covers about What Is -3x + 1 Subtracted From 3x - 1 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.