What Is 30 1 3 Of 3
Juapaving
May 10, 2025 · 5 min read
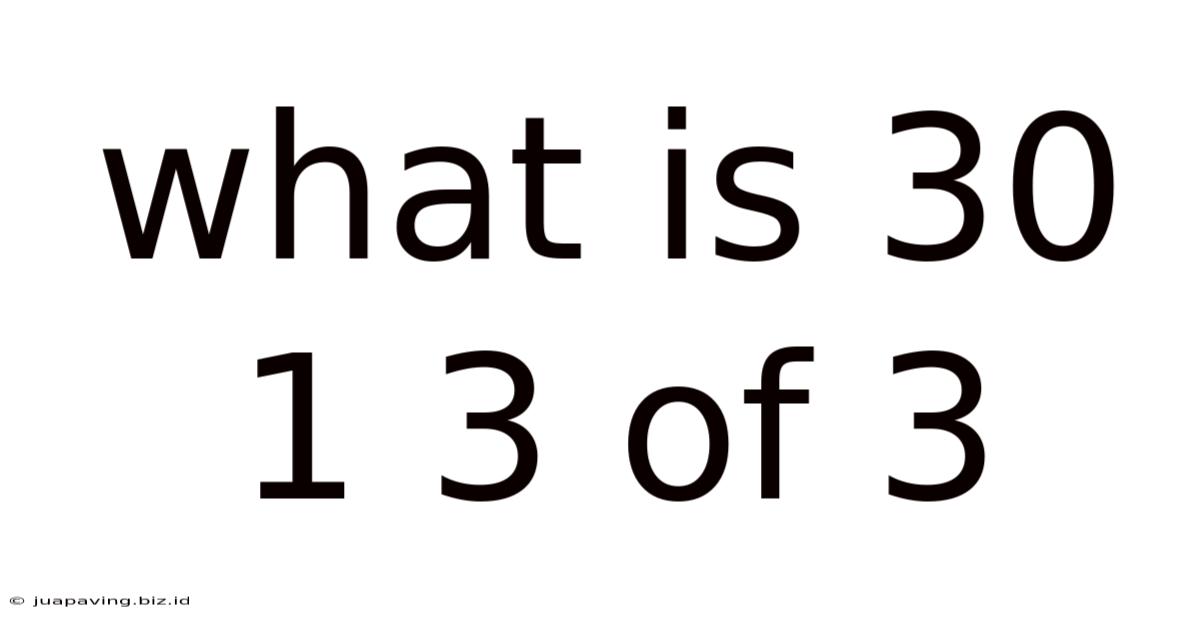
Table of Contents
What is 30 1 3 of 3? Unraveling the Enigma of Mathematical Expressions
The seemingly simple expression "30 1 3 of 3" presents a puzzle that requires careful interpretation and understanding of mathematical operations. At first glance, it appears ambiguous, lacking explicit operators to guide the calculation. However, by exploring various possibilities and applying standard mathematical conventions, we can arrive at a solution and delve into the broader context of interpreting ambiguous mathematical notation.
Understanding the Problem: The Ambiguity of the Expression
The core challenge lies in the absence of clearly defined operators between the numbers. Standard mathematical notation utilizes symbols like +, -, ×, and ÷ to denote addition, subtraction, multiplication, and division respectively. The lack of these symbols leaves room for multiple interpretations, each yielding a different result. This ambiguity highlights the crucial role of clear and unambiguous notation in mathematics to avoid misinterpretations and ensure accurate calculations.
Possible Interpretations and Their Solutions
Let's explore several ways we might interpret "30 1 3 of 3":
1. Interpretation as a Series of Operations:
One interpretation is to treat the expression as a series of operations, potentially involving implied multiplication. We could interpret "of" as multiplication, leading to:
- 30 - 1 + (3 x 3) = 30 - 1 + 9 = 38
This interpretation assumes a specific order of operations (subtraction, then addition, then multiplication). It prioritizes multiplication over addition and subtraction, adhering to standard order of operations (PEMDAS/BODMAS).
2. Interpretation as a Mixed Number:
Another possibility is to interpret "30 1 3" as a mixed number, where "30" is the whole number part, and "1 3" represents a fraction. This would then be multiplied by 3:
- (30 + (1/3)) x 3 = 30 + 1 = 31
This interpretation assumes familiarity with mixed number representation and treats "of" as multiplication.
3. Interpretation Involving Concatenation and Operations:
A more abstract interpretation could involve concatenation of numbers followed by operations. This approach could be arbitrarily complex, demonstrating the importance of precise notation. For instance:
- (3013 / 3) = 1004.333... This interprets the numbers as a single, four-digit number divided by 3.
However, this interpretation lacks an explicit justification within standard mathematical practices. While possible, it's far less intuitive and relies on making significant assumptions about the intended meaning.
4. Considering Context: The Importance of Clarity in Mathematics
The ambiguity of the original expression highlights a critical point: mathematical notation needs to be precise and unambiguous to prevent misinterpretations. The lack of clarity in "30 1 3 of 3" could stem from several sources:
- Typographical Errors: A simple typing mistake could have omitted essential operators.
- Informal Notation: The expression might be used in an informal setting where precise notation isn't strictly followed.
- Coded Language: While unlikely, the expression could be part of a coded language or puzzle where the symbols have a non-standard meaning.
5. Applying the Order of Operations (PEMDAS/BODMAS):
The principle of the order of operations (often remembered by the acronyms PEMDAS – Parentheses, Exponents, Multiplication and Division, Addition and Subtraction, or BODMAS – Brackets, Orders, Division and Multiplication, Addition and Subtraction) is crucial when evaluating mathematical expressions. Without explicit parentheses or other grouping symbols, we typically apply these rules. However, the absence of standard operators in "30 1 3 of 3" makes a direct application of PEMDAS/BODMAS challenging.
Extending the Discussion: Mathematical Notation and Its Significance
The seemingly simple puzzle of "30 1 3 of 3" serves as a valuable case study in the importance of clear mathematical notation. Ambiguous expressions can lead to confusion, errors, and misinterpretations, particularly in fields like programming, engineering, and scientific research, where accuracy is paramount.
The Role of Symbols and Conventions in Mathematics
Mathematics relies heavily on a standardized system of symbols and conventions. These conventions ensure that mathematical expressions have a unique and unambiguous meaning, regardless of the interpreter. The use of standard operators, parentheses, brackets, and other notation aids in correctly ordering operations and grouping terms.
The Impact of Ambiguity in Real-World Applications
Ambiguous notation can have severe consequences in various contexts:
- Software Development: In programming, a simple typographical error or misunderstanding of operator precedence can lead to software bugs, malfunctioning systems, or unexpected outputs.
- Engineering and Design: Ambiguity in engineering drawings or calculations could lead to structural failures, equipment malfunctions, or other critical errors.
- Scientific Research: Inaccurate calculations or misinterpreted data due to ambiguous notation can lead to flawed research results, erroneous conclusions, and wasted resources.
Best Practices for Clear Mathematical Notation
To avoid ambiguity and ensure accuracy, always adhere to the following best practices:
- Use Standard Operators: Explicitly include the appropriate operators (+, -, ×, ÷) to indicate addition, subtraction, multiplication, and division.
- Use Parentheses: Use parentheses or brackets to group terms and indicate the order of operations.
- Define Variables: If using variables, clearly define their meaning and units.
- Maintain Consistency: Be consistent in your notation and terminology throughout your calculations or expressions.
- Review and Check: Always review your work and check for errors or potential ambiguities before making any decisions or drawing conclusions based on the calculations.
Conclusion: Learning from the Ambiguity
The seemingly trivial puzzle of "30 1 3 of 3" highlights the importance of clear, unambiguous mathematical notation. The multiple interpretations and resulting varied solutions underscore the critical role of precise communication in mathematics and its applications. By adopting best practices for mathematical notation and rigorously adhering to conventions like the order of operations, we can minimize the risk of errors and ensure the accurate and consistent interpretation of mathematical expressions. The puzzle serves as a valuable reminder that even seemingly simple expressions can hold significant ambiguity if not carefully and precisely defined. The lesson learned is to always prioritize clarity and precision in mathematical notation to avoid costly mistakes and ensure reliable results.
Latest Posts
Latest Posts
-
What Is The Distance Around A Shape Called
May 10, 2025
-
What Is The Molar Mass Of H2s
May 10, 2025
-
A Quadrilateral With 1 Set Of Parallel Sides
May 10, 2025
-
What Are The Boiling And Freezing Points Of Water
May 10, 2025
-
A Tissue That Has A Fluid Matrix Is
May 10, 2025
Related Post
Thank you for visiting our website which covers about What Is 30 1 3 Of 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.