What Is 3 Out Of 25 As A Percentage
Juapaving
May 12, 2025 · 5 min read
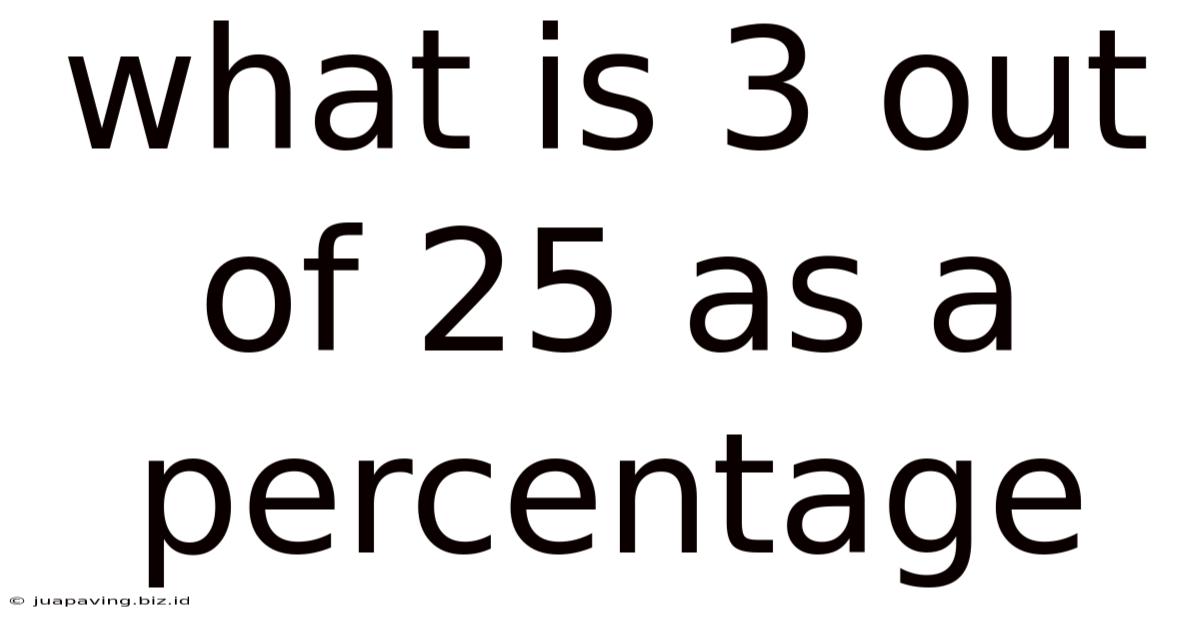
Table of Contents
What is 3 out of 25 as a Percentage? A Comprehensive Guide
Calculating percentages is a fundamental skill with wide-ranging applications in various aspects of life, from everyday finances to complex statistical analyses. Understanding how to convert fractions into percentages is crucial for making informed decisions and interpreting data accurately. This article will delve into the calculation of "3 out of 25 as a percentage," exploring various methods, offering practical examples, and clarifying common misconceptions. We'll also examine the broader context of percentage calculations and their importance in different fields.
Understanding the Basics: Fractions, Decimals, and Percentages
Before we dive into the specific calculation, let's establish a solid understanding of the fundamental relationships between fractions, decimals, and percentages.
-
Fraction: A fraction represents a part of a whole. It consists of a numerator (the top number) and a denominator (the bottom number). In our case, "3 out of 25" is represented as the fraction 3/25.
-
Decimal: A decimal is a way of expressing a fraction using a base-10 system. It uses a decimal point to separate the whole number part from the fractional part.
-
Percentage: A percentage is a fraction expressed as a portion of 100. It's denoted by the symbol "%". A percentage represents a proportion relative to a whole, often used to express rates, ratios, or changes.
The core concept is that fractions, decimals, and percentages are simply different ways of representing the same numerical value. They are interchangeable, and understanding their interconversion is crucial for mathematical fluency.
Method 1: Converting the Fraction to a Decimal
The most straightforward method to calculate "3 out of 25" as a percentage involves first converting the fraction into a decimal and then multiplying by 100.
-
Divide the numerator by the denominator: Divide 3 (numerator) by 25 (denominator). This gives us 0.12.
-
Multiply by 100: Multiply the decimal (0.12) by 100 to convert it to a percentage. This yields 12.
Therefore, 3 out of 25 is 12%.
Method 2: Using Proportions
This method utilizes the concept of proportions to directly calculate the percentage. We set up a proportion where we know one part (3 out of 25) and want to find the equivalent proportion out of 100.
-
Set up the proportion: We set up the proportion as follows:
3/25 = x/100
Where 'x' represents the percentage we want to find.
-
Cross-multiply: Cross-multiply the equation:
25x = 300
-
Solve for x: Divide both sides by 25:
x = 12
Therefore, 3 out of 25 is 12%.
Method 3: Simplifying the Fraction First (Optional)
While not strictly necessary, simplifying the fraction before conversion can sometimes make the calculation easier. In this case, 3/25 cannot be simplified further because 3 and 25 do not share any common factors other than 1. However, let's examine a scenario where simplification is beneficial.
Consider the fraction 6/50. This fraction can be simplified by dividing both the numerator and the denominator by 2, resulting in 3/25. From there, you can use either Method 1 or Method 2 to determine the percentage (which, as we've established, is 12%).
Practical Applications: Real-World Examples
Understanding percentage calculations is crucial in various real-world scenarios. Here are a few examples showcasing the practical application of calculating "3 out of 25 as a percentage":
-
Test Scores: If a student answered 3 questions correctly out of a total of 25 questions on a test, their score would be 12%.
-
Sales and Discounts: A store might offer a 12% discount on an item, implying a reduction of 3 units out of every 25 units sold.
-
Survey Results: If 3 out of 25 respondents chose a particular option in a survey, that option represents 12% of the responses.
-
Financial Calculations: Calculating interest rates, returns on investments, or changes in stock prices often involves percentage calculations.
-
Data Analysis: In data analysis, percentages are commonly used to represent proportions within datasets, allowing for easier comparisons and interpretations.
Advanced Concepts and Further Exploration
While calculating "3 out of 25 as a percentage" is a relatively simple calculation, mastering percentages opens doors to more complex mathematical concepts:
-
Compound Interest: This involves calculating interest on both the principal amount and accumulated interest, leading to exponential growth.
-
Statistical Analysis: Percentages are used extensively in statistical analysis, particularly in calculating probabilities, frequencies, and confidence intervals.
-
Financial Modeling: Sophisticated financial models rely on percentage calculations to project future performance, assess risks, and make investment decisions.
-
Data Visualization: Percentages are frequently used in charts and graphs to visually represent proportions and trends within datasets.
Common Mistakes and How to Avoid Them
Several common mistakes can arise when calculating percentages. Being aware of these pitfalls is crucial for accurate calculations:
-
Incorrect Order of Operations: Always ensure you perform the division before multiplication when converting a fraction to a percentage.
-
Misunderstanding Decimal Places: Pay close attention to decimal places when converting decimals to percentages, ensuring you multiply by 100 correctly.
-
Using Incorrect Formulas: Double-check the formula you are using and ensure you understand the underlying principles.
-
Improper Simplification: While simplifying fractions can be helpful, ensure you simplify correctly to avoid errors in subsequent calculations.
Conclusion: Mastering Percentage Calculations
Calculating "3 out of 25 as a percentage" (12%) might seem like a simple task, but it highlights the importance of understanding the fundamental principles of fractions, decimals, and percentages. These concepts are essential for a wide range of applications, from basic arithmetic to complex financial modeling and statistical analysis. Mastering these techniques provides a solid foundation for tackling more advanced mathematical challenges and enhancing your ability to interpret and analyze data effectively in various contexts. By understanding the methods presented here and being mindful of common mistakes, you'll be well-equipped to confidently handle percentage calculations in your daily life and professional endeavors. Remember that practice is key to solidifying your understanding and building confidence in your mathematical skills.
Latest Posts
Latest Posts
-
What Is The Primary Electron Acceptor In Photosynthesis
May 12, 2025
-
A Rigid Body Is Made Of Three Identical
May 12, 2025
-
What Is The Storage Form Of Glucose In Plants
May 12, 2025
-
Lead Ii Nitrate And Sodium Chloride
May 12, 2025
-
The Most Inclusive Biological Taxon Is The
May 12, 2025
Related Post
Thank you for visiting our website which covers about What Is 3 Out Of 25 As A Percentage . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.