What Is 3 As A Percentage Of 25
Juapaving
May 12, 2025 · 4 min read
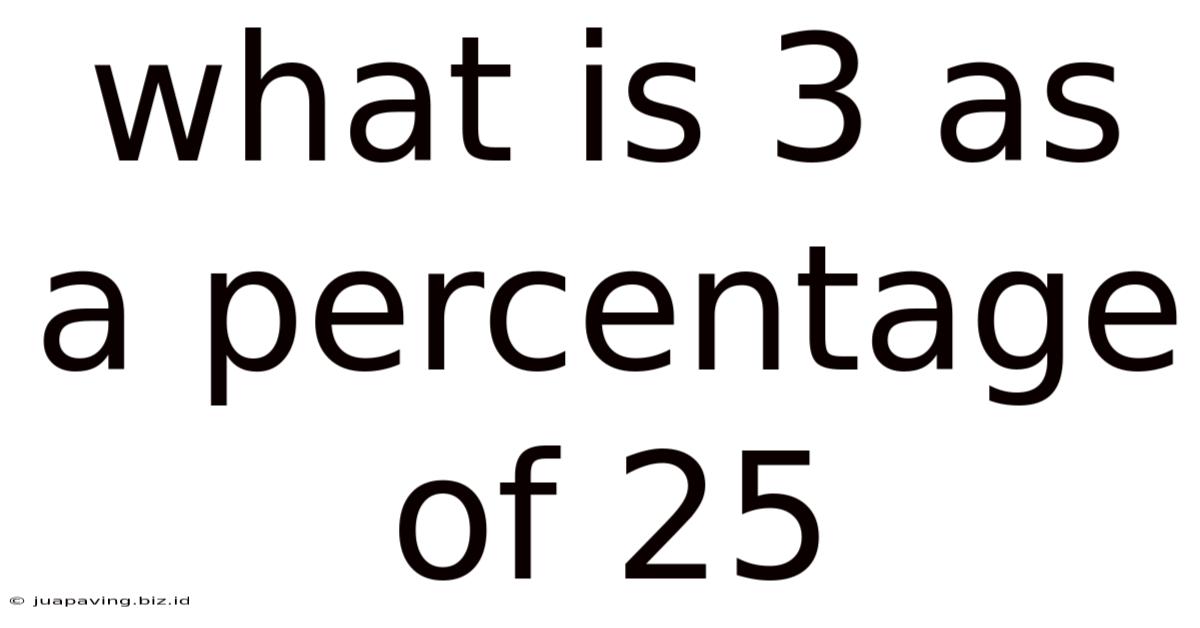
Table of Contents
What is 3 as a Percentage of 25? A Comprehensive Guide to Percentage Calculations
Understanding percentages is a fundamental skill in numerous aspects of life, from calculating discounts and taxes to analyzing financial data and understanding statistics. This comprehensive guide will delve into the question, "What is 3 as a percentage of 25?", and explore the broader concepts of percentage calculations, providing you with the tools and knowledge to confidently tackle similar problems.
Understanding Percentages: The Basics
A percentage is a way of expressing a number as a fraction of 100. The term "percent" literally means "out of 100" ("per cent" – per hundred). This means that 50% is equivalent to 50/100, which simplifies to 1/2 or 0.5. Percentages are useful because they allow us to easily compare proportions and fractions, making complex data more digestible and understandable.
Calculating Percentages: The Formula
The fundamental formula for calculating a percentage is:
(Part / Whole) * 100% = Percentage
Where:
- Part: Represents the specific portion you're interested in expressing as a percentage.
- Whole: Represents the total amount or the complete quantity.
- Percentage: The resulting value expressed as a percentage.
Let's apply this formula to our core question: "What is 3 as a percentage of 25?"
In this case:
- Part = 3
- Whole = 25
Substituting these values into the formula:
(3 / 25) * 100% = Percentage
This simplifies to:
(0.12) * 100% = 12%
Therefore, 3 is 12% of 25.
Step-by-Step Calculation: A Detailed Approach
To further solidify understanding, let's break down the calculation step-by-step:
-
Divide the part by the whole: Divide 3 by 25 (3 ÷ 25 = 0.12). This gives you the decimal representation of the fraction.
-
Multiply by 100: Multiply the decimal result (0.12) by 100 to convert it into a percentage (0.12 * 100 = 12).
-
Add the percentage symbol: Finally, add the "%" symbol to indicate that the result is a percentage.
Practical Applications: Real-World Examples
Understanding percentage calculations is crucial in various real-world scenarios. Here are a few examples to illustrate its practical application:
1. Sales and Discounts:
Imagine a store offering a 20% discount on an item originally priced at $50. To calculate the discount, you would use the same percentage formula:
(20/100) * $50 = $10
The discount is $10, making the final price $40.
2. Tax Calculations:
If the sales tax in your area is 6%, and you purchase an item for $75, you can calculate the tax amount as follows:
(6/100) * $75 = $4.50
The sales tax will be $4.50.
3. Grade Calculations:
In an exam with 25 questions, if you answer 18 correctly, your percentage score would be:
(18/25) * 100% = 72%
Your score would be 72%.
4. Financial Analysis:
Percentage calculations are essential for interpreting financial statements. For instance, calculating profit margins, return on investment (ROI), and growth rates all rely on understanding and applying percentages.
Beyond the Basics: Advanced Percentage Calculations
While the fundamental formula provides a solid base, more complex scenarios may require adjustments or additional steps. These include:
-
Calculating the whole when given the percentage and part: If you know that 15% of a number is 6, you can find the whole number using algebraic manipulation of the percentage formula.
-
Calculating percentage increase or decrease: This involves comparing two values over time to determine the percentage change. The formula is:
((New Value - Old Value) / Old Value) * 100%. -
Compounding percentages: This is crucial in areas like finance, where interest is calculated on both the principal amount and accumulated interest.
Tips and Tricks for Accurate Percentage Calculations
-
Use a calculator: For complex calculations, a calculator will ensure accuracy and efficiency.
-
Check your work: Always double-check your calculations to avoid errors. Try working backward from your answer to confirm its validity.
-
Master the decimal conversion: A firm understanding of converting decimals to percentages and vice versa is fundamental.
-
Practice regularly: The more you practice solving percentage problems, the more confident and efficient you'll become.
Conclusion: Mastering Percentages for Success
Understanding how to calculate percentages is a versatile skill with far-reaching applications in various fields. This guide has provided a comprehensive overview of percentage calculations, from the basic formula to more advanced techniques. By grasping these concepts and practicing regularly, you will confidently approach any percentage-related problem, improving your analytical skills and decision-making abilities. Remember the core formula: (Part / Whole) * 100% = Percentage, and you'll be well-equipped to tackle any percentage calculation you encounter. Keep practicing, and you'll master this essential mathematical skill.
Latest Posts
Latest Posts
-
1 Out Of 13 As A Percentage
May 12, 2025
-
What Is The Lcm Of 20 And 18
May 12, 2025
-
2 Pairs Of Opposite Sides That Are Parallel
May 12, 2025
-
What Do The Arrows Show In A Food Chain
May 12, 2025
-
Lichens Are Symbiotic Associations Of Fungi And
May 12, 2025
Related Post
Thank you for visiting our website which covers about What Is 3 As A Percentage Of 25 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.