What Is 3/8 As A Mixed Number
Juapaving
May 12, 2025 · 6 min read
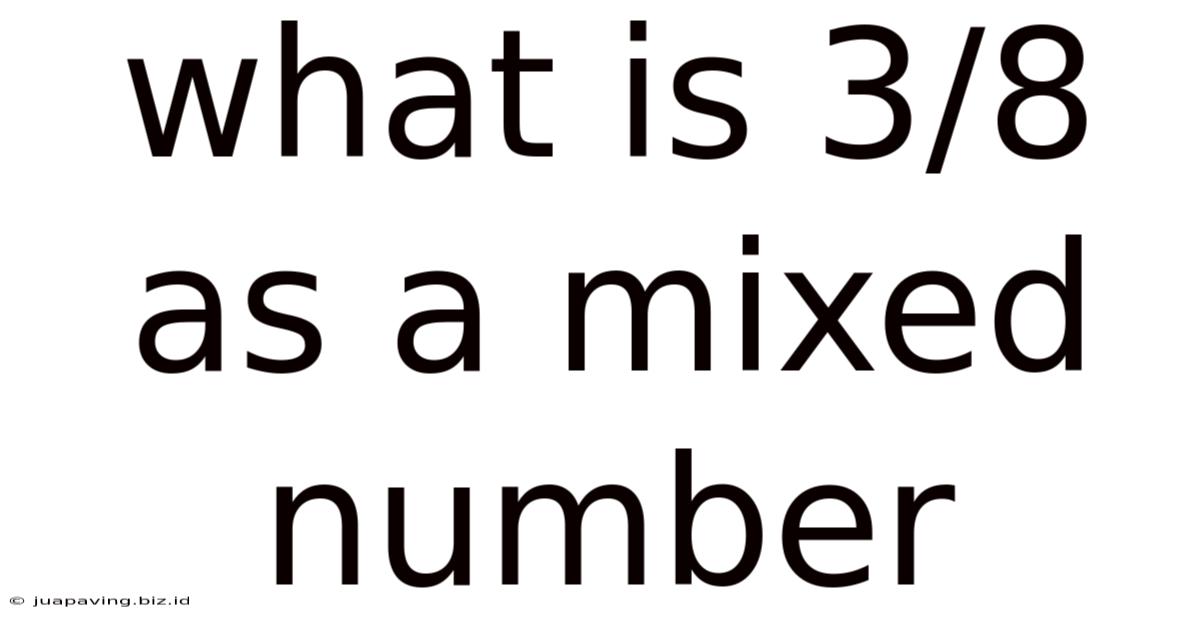
Table of Contents
What is 3/8 as a Mixed Number? A Comprehensive Guide
Understanding fractions is a fundamental skill in mathematics, essential for various applications from everyday calculations to advanced scientific concepts. One common task involving fractions is converting improper fractions (where the numerator is larger than or equal to the denominator) into mixed numbers (a combination of a whole number and a proper fraction). This article delves into the conversion process, focusing specifically on converting the improper fraction 3/8 into a mixed number and providing a broader understanding of fraction manipulation.
Understanding Fractions: A Quick Refresher
Before diving into the conversion, let's briefly review the components of a fraction:
- Numerator: The top number in a fraction, representing the number of parts we have.
- Denominator: The bottom number in a fraction, indicating the total number of equal parts that make up a whole.
An improper fraction is a fraction where the numerator is greater than or equal to the denominator (e.g., 7/4, 5/5, 9/2). A proper fraction is one where the numerator is less than the denominator (e.g., 1/2, 3/4, 2/5). A mixed number combines a whole number and a proper fraction (e.g., 1 ¾, 2 ⅓, 3 ⅛).
Converting 3/8 to a Mixed Number: The Process
The fraction 3/8 is a proper fraction; the numerator (3) is less than the denominator (8). Therefore, it cannot be converted into a mixed number. 3/8 remains as 3/8. There is no whole number component because 3 is smaller than 8; it doesn't represent a complete whole. To illustrate the conversion process, let's consider an example of an improper fraction that can be converted.
Let's take the improper fraction 11/4. To convert it into a mixed number:
-
Divide the numerator by the denominator: 11 ÷ 4 = 2 with a remainder of 3.
-
The quotient becomes the whole number part of the mixed number: The quotient is 2.
-
The remainder becomes the numerator of the fractional part: The remainder is 3.
-
The denominator remains the same: The denominator stays as 4.
Therefore, 11/4 as a mixed number is 2 ¾.
Why We Convert Fractions
Converting between improper fractions and mixed numbers offers several advantages:
-
Improved Understanding: Mixed numbers often provide a more intuitive representation of quantities, making them easier to grasp visually and conceptually. For example, 2 ¾ pizzas is more easily understood than 11/4 pizzas.
-
Simplification of Calculations: In some calculations, working with mixed numbers can be more efficient than dealing with improper fractions. For instance, adding mixed numbers can be simpler than adding improper fractions, especially when the denominators are different.
-
Real-World Applications: Mixed numbers are frequently encountered in daily life, from measuring ingredients in cooking to calculating distances and times. Understanding the conversion helps us relate mathematical concepts to practical situations.
Other Fraction Conversions: Exploring Related Concepts
Beyond the conversion of improper fractions to mixed numbers, various other fraction manipulations are crucial for a comprehensive understanding of fractions:
1. Simplifying Fractions (Reducing to Lowest Terms)
Simplifying a fraction involves finding an equivalent fraction with a smaller numerator and denominator. This is done by dividing both the numerator and denominator by their greatest common divisor (GCD). For example, simplifying 6/12:
- The GCD of 6 and 12 is 6.
- Dividing both the numerator and denominator by 6 gives 1/2.
Therefore, 6/12 simplified is 1/2.
2. Adding and Subtracting Fractions
Adding and subtracting fractions requires a common denominator. If the fractions have the same denominator, simply add or subtract the numerators and keep the denominator the same. If the denominators are different, find the least common multiple (LCM) of the denominators, convert the fractions to equivalent fractions with the LCM as the denominator, and then add or subtract the numerators.
3. Multiplying and Dividing Fractions
Multiplying fractions involves multiplying the numerators together and multiplying the denominators together. Dividing fractions involves inverting the second fraction (reciprocal) and then multiplying the two fractions.
4. Converting Decimals to Fractions and Vice Versa
Decimals can be converted to fractions by writing the decimal as a fraction with a denominator that is a power of 10 (e.g., 0.75 = 75/100). Fractions can be converted to decimals by performing the division indicated by the fraction (e.g., 1/4 = 0.25).
The Significance of Mastering Fraction Conversion
Mastering fraction conversion, including converting between improper fractions and mixed numbers, is paramount for success in mathematics and its various applications. It forms the foundation for more advanced mathematical concepts, including algebra, calculus, and geometry. A strong understanding of fractions is also essential for success in various fields, such as engineering, finance, and computer science.
Practical Applications of Fraction Conversion
The ability to work confidently with fractions, particularly in converting between improper fractions and mixed numbers, manifests itself in numerous everyday scenarios:
-
Cooking and Baking: Recipes often utilize fractions for precise ingredient measurements. Converting between improper fractions and mixed numbers allows for easier interpretation and measurement of ingredients.
-
Construction and Carpentry: Accurate measurements are crucial in construction and carpentry. Understanding fractions is essential for precise cutting and fitting of materials.
-
Sewing and Tailoring: Patterns and measurements in sewing and tailoring frequently employ fractions. Converting fractions ensures accurate fabric cutting and garment construction.
-
Finance and Budgeting: Managing finances and budgets often involves working with fractions and percentages. Understanding fraction conversion is vital for accurate calculations and financial planning.
-
Data Analysis and Statistics: In data analysis and statistics, fractions are frequently used to represent proportions and probabilities. The ability to convert fractions improves the understanding and interpretation of data.
Troubleshooting Common Mistakes
While converting fractions might seem straightforward, several common errors can occur:
-
Incorrect Division: When converting an improper fraction to a mixed number, ensure accurate division of the numerator by the denominator. A mistake in the division will lead to an incorrect mixed number.
-
Misplacing the Remainder: The remainder from the division should become the numerator of the fractional part of the mixed number. Putting the remainder in the wrong place will yield an incorrect result.
-
Forgetting to Simplify: After converting an improper fraction, always check if the resulting fractional part can be simplified. Simplifying the fraction ensures the answer is in its most concise form.
-
Confusing Numerator and Denominator: Always ensure that the numerator (top number) and denominator (bottom number) are correctly identified and placed in the fraction.
Conclusion: Embracing the Power of Fractions
The conversion of fractions, especially from improper fractions to mixed numbers, is a fundamental skill with wide-ranging applications. While the example of 3/8, being a proper fraction, doesn't require conversion, understanding the process and its application to other fractions equips you with a crucial tool for various mathematical and real-world scenarios. By mastering fraction manipulation, you pave the way for success in more advanced mathematical concepts and navigate various practical situations with confidence and accuracy. Consistent practice and attention to detail will solidify your understanding and lead to proficiency in handling fractions effectively.
Latest Posts
Latest Posts
-
2 1 3 As A Percent
May 12, 2025
-
Is Iron An Element Or A Compound
May 12, 2025
-
Which Of The Following Numbers Are Irrational
May 12, 2025
-
Can Light Waves Travel Through A Vacuum
May 12, 2025
-
Picture Of Concave And Convex Mirror
May 12, 2025
Related Post
Thank you for visiting our website which covers about What Is 3/8 As A Mixed Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.