What Is 3/20 As A Percentage
Juapaving
May 12, 2025 · 4 min read
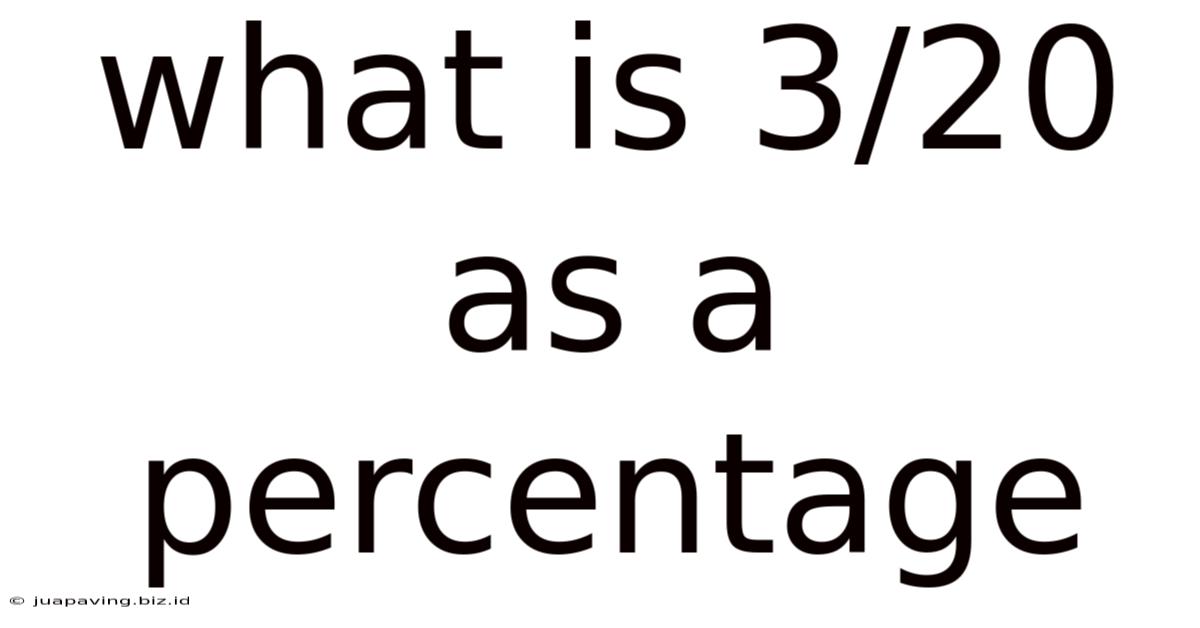
Table of Contents
What is 3/20 as a Percentage? A Comprehensive Guide
Converting fractions to percentages is a fundamental skill in mathematics with wide-ranging applications in everyday life, from calculating discounts and taxes to understanding statistics and financial data. This comprehensive guide will delve into the process of converting the fraction 3/20 into a percentage, exploring various methods and providing a deeper understanding of the underlying concepts. We'll also look at practical applications and related percentage calculations to solidify your understanding.
Understanding Fractions and Percentages
Before we jump into the conversion, let's briefly review the basics of fractions and percentages.
Fractions: A fraction represents a part of a whole. It's expressed as a ratio of two numbers: the numerator (top number) and the denominator (bottom number). In our case, 3/20 means 3 parts out of a total of 20 parts.
Percentages: A percentage is a way of expressing a number as a fraction of 100. The symbol "%" signifies "per hundred." For example, 50% means 50 out of 100, or 50/100, which simplifies to 1/2.
Method 1: Direct Conversion using Division
The most straightforward method to convert a fraction to a percentage involves dividing the numerator by the denominator and then multiplying the result by 100.
Steps:
- Divide the numerator by the denominator: 3 ÷ 20 = 0.15
- Multiply the result by 100: 0.15 × 100 = 15
Therefore, 3/20 as a percentage is 15%.
This method is simple and efficient, particularly for fractions with relatively small numbers.
Method 2: Converting to an Equivalent Fraction with a Denominator of 100
Another approach involves finding an equivalent fraction where the denominator is 100. This directly gives you the percentage since percentages are fractions out of 100.
Steps:
- Determine the factor to multiply the denominator by to get 100: 100 ÷ 20 = 5
- Multiply both the numerator and the denominator by this factor: (3 × 5) / (20 × 5) = 15/100
- Express the fraction as a percentage: 15/100 = 15%
This method highlights the direct relationship between fractions and percentages and is particularly useful for fractions with denominators that are factors of 100 (like 20, 25, 50).
Method 3: Using Proportions
This method utilizes the concept of proportions to solve the problem. We set up a proportion where one ratio represents the fraction and the other represents the percentage (out of 100).
Steps:
- Set up a proportion: 3/20 = x/100
- Cross-multiply: 20x = 300
- Solve for x: x = 300 ÷ 20 = 15
Therefore, x = 15%, which is 3/20 as a percentage.
This method is valuable for understanding the underlying proportional relationships between fractions and percentages. It is a more general method that can be applied to a wider range of fraction-to-percentage conversions.
Practical Applications of Percentage Conversions
Understanding how to convert fractions to percentages is crucial in many real-world scenarios:
- Discounts: A store offers a 3/20 discount on an item. Knowing that 3/20 = 15% allows you to easily calculate the discount amount.
- Taxes: If a sales tax is 3/20, you can quickly calculate the tax on a purchase by multiplying the price by 15%.
- Financial Analysis: Converting fractions representing financial ratios (like profit margins or debt-to-equity ratios) to percentages makes them easier to understand and compare.
- Statistics: Many statistical measures are expressed as percentages, requiring conversion from fractions or decimals.
- Surveys and Polls: Results of surveys and polls are often presented as percentages, necessitating the conversion of raw data (often in fractional form).
- Grade Calculations: In some grading systems, scores might be represented as fractions, which then need to be converted to percentages.
Related Percentage Calculations
Building upon the conversion of 3/20 to 15%, let's explore some related percentage calculations:
-
Finding a percentage of a number: To find 15% of a number, say 200, you would multiply 200 by 0.15 (which is 15% as a decimal): 200 × 0.15 = 30. Therefore, 15% of 200 is 30.
-
Calculating percentage increase or decrease: If a quantity increases from 200 to 230, the percentage increase is calculated as follows: [(230 - 200) / 200] × 100% = 15%. Similarly, if it decreases from 200 to 170, the percentage decrease would be [(200 - 170) / 200] × 100% = 15%.
-
Finding the original value after a percentage change: If a number is increased by 15% to 230, you can find the original value by dividing 230 by 1.15 (1 + 0.15): 230 ÷ 1.15 = 200. This works similarly for percentage decreases.
Conclusion
Converting fractions to percentages is a vital mathematical skill with many practical applications. The conversion of 3/20 to 15% can be achieved through several methods, each offering a unique approach to understanding the underlying concept. Mastering these methods and related percentage calculations empowers you to confidently tackle various mathematical and real-world problems involving fractions and percentages. This knowledge is crucial for making informed decisions in various aspects of daily life, from personal finance to professional analysis. Remember to practice these methods with different fractions to solidify your understanding and improve your problem-solving skills.
Latest Posts
Latest Posts
-
Power And Power Factor In Ac Circuits
May 12, 2025
-
What Unit Is Acceleration Measured In
May 12, 2025
-
Kelvin Planck Statement Of The Second Law Of Thermodynamics
May 12, 2025
-
Is 73 A Prime Or Composite Number
May 12, 2025
-
Standard Form Of A Polynomial Definition Math
May 12, 2025
Related Post
Thank you for visiting our website which covers about What Is 3/20 As A Percentage . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.