What Is 20 Percent Of 50
Juapaving
May 14, 2025 · 5 min read
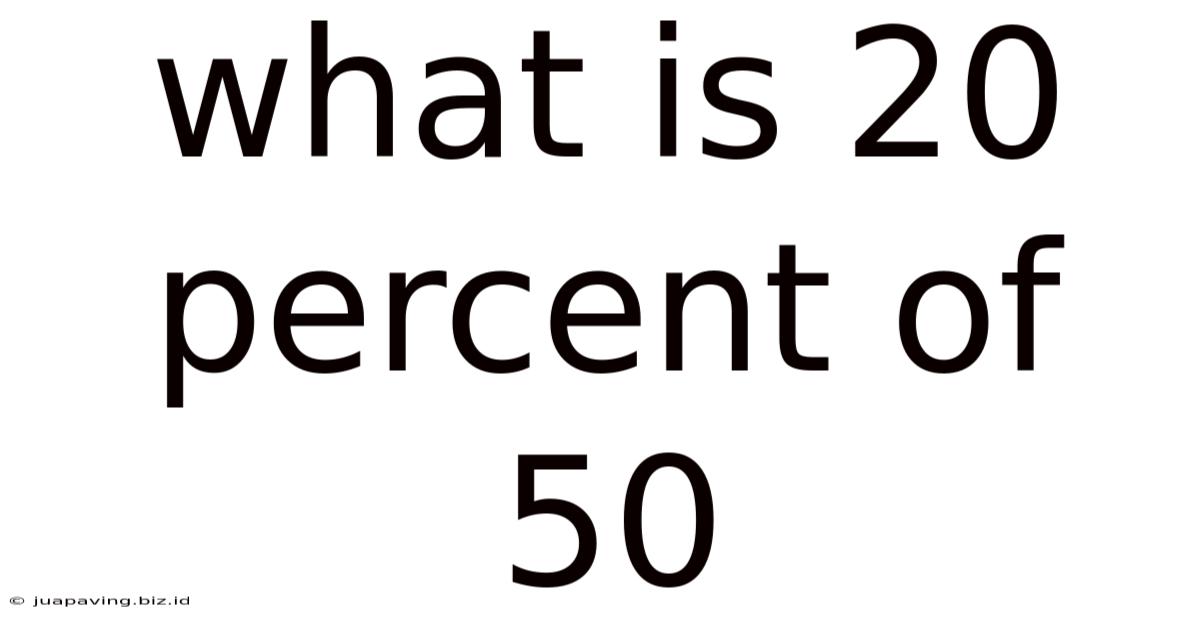
Table of Contents
What is 20 Percent of 50? A Deep Dive into Percentages and Their Applications
Calculating percentages is a fundamental skill with widespread applications in everyday life, from calculating discounts and sales tax to understanding financial reports and statistical data. This article will delve into the simple calculation of "What is 20 percent of 50?" and then expand upon the broader concepts of percentages, their practical uses, and how to master them.
Understanding Percentages: The Basics
A percentage is a fraction or ratio expressed as a number out of 100. The word "percent" literally means "out of one hundred." The symbol "%" is used to represent percentages. Therefore, 20% means 20 out of 100, which can be written as the fraction 20/100 or the decimal 0.20.
Calculating 20 Percent of 50
The calculation of 20% of 50 is straightforward. There are several methods to achieve this:
Method 1: Using Decimal Conversion
- Convert the percentage to a decimal: 20% = 0.20
- Multiply the decimal by the number: 0.20 * 50 = 10
Therefore, 20% of 50 is $\boxed{10}$.
Method 2: Using Fraction Conversion
- Convert the percentage to a fraction: 20% = 20/100 = 1/5
- Multiply the fraction by the number: (1/5) * 50 = 10
Again, 20% of 50 is $\boxed{10}$.
Method 3: Proportion Method
This method is useful for understanding the underlying relationship between percentages and proportions. We can set up a proportion:
- 20/100 = x/50
Where 'x' represents the unknown value (20% of 50). To solve for x, we cross-multiply:
- 100x = 20 * 50
- 100x = 1000
- x = 10
Thus, 20% of 50 is $\boxed{10}$.
Real-World Applications of Percentage Calculations
Understanding percentages is crucial in numerous real-world situations. Here are some examples:
1. Sales and Discounts:
Stores frequently advertise discounts as percentages. For instance, a "20% off" sale means you'll pay 80% of the original price. Knowing how to calculate percentages helps you quickly determine the final price after a discount. For example, if an item costs $50 and is 20% off, the discount is $10 (as we've already calculated), and the final price is $40.
2. Taxes and Tips:
Sales tax and tips are often expressed as percentages. Calculating these percentages helps you determine the total cost of a purchase or the appropriate tip amount in a restaurant. For example, a 6% sales tax on a $50 purchase would be $3 (6% of $50 = $3), resulting in a total cost of $53.
3. Financial Analysis:
Percentages are essential in financial analysis. Investors use percentages to analyze returns on investments, growth rates, and profit margins. Understanding percentage changes helps assess the performance of stocks, bonds, and other investments. For example, if an investment grows from $50 to $60, the percentage increase is 20% (($10/$50)*100%).
4. Statistics and Data Analysis:
Percentages are widely used in statistics to represent proportions and frequencies within datasets. For example, in a survey of 100 people, if 20 responded positively to a question, the positive response rate is 20%. Understanding percentages facilitates interpretation and comparison of data.
5. Grade Calculations:
In education, percentages are used to represent grades and scores. A score of 10 out of 50, for instance, is equivalent to 20%. This allows for easy comparison of student performance across different assignments and assessments.
Mastering Percentage Calculations: Tips and Tricks
While the basic calculations are relatively simple, mastering percentages involves understanding different scenarios and developing efficient calculation methods.
1. Memorizing Common Percentages:
Memorizing the decimal and fraction equivalents of common percentages (like 10%, 20%, 25%, 50%, 75%, and 100%) can significantly speed up calculations.
2. Using Mental Math Techniques:
Practice mental math techniques to quickly calculate percentages. For example, 10% of a number is simply moving the decimal point one place to the left. 20% is double that, 50% is half the number, and so on.
3. Utilizing Calculators and Spreadsheets:
For more complex percentage calculations, utilize calculators or spreadsheet software like Microsoft Excel or Google Sheets. These tools can handle more intricate calculations quickly and accurately.
4. Practicing Regularly:
Consistent practice is key to mastering percentage calculations. Work through various examples and problems to build your confidence and improve your speed and accuracy.
5. Understanding Percentage Increase and Decrease:
Pay close attention to the context. A 20% increase and a 20% decrease from the same starting point will result in different final values. Understanding how to calculate these changes accurately is critical in many applications.
Beyond the Basics: More Complex Percentage Problems
While finding 20% of 50 is a simple calculation, percentage problems can become more complex. Understanding these complexities is essential for advanced applications.
1. Finding the Original Value:
Sometimes you know the percentage and the resulting value, but need to find the original value. For instance, if a discounted price is $40 after a 20% discount, you would need to work backward to find the original price of $50. This involves using algebraic equations to solve for the unknown value.
2. Calculating Percentage Change:
Percentage change involves determining the percentage increase or decrease between two values. This often requires subtracting the initial value from the final value, dividing the result by the initial value, and then multiplying by 100% to express it as a percentage.
3. Compound Interest:
Compound interest is a more complex application of percentages, where interest earned in one period is added to the principal, and the next period's interest is calculated on the new, larger amount. This compounding effect leads to exponential growth over time.
4. Percentage Points vs. Percentages:
It's crucial to distinguish between percentage points and percentages. A change from 20% to 30% is a 10 percentage point increase, but it's a 50% increase (10/20 * 100%). This distinction is often overlooked but vital for accurate interpretation.
Conclusion: The Ubiquity of Percentages
Understanding percentages is a crucial life skill with applications spanning numerous fields. From everyday shopping to complex financial analysis, mastering percentage calculations empowers you to make informed decisions, interpret data accurately, and navigate the numerical world with confidence. While the simple calculation of "What is 20 percent of 50?" serves as a foundational stepping stone, exploring the broader concepts and mastering more complex problems unlocks a world of opportunities. By consistently practicing and utilizing various techniques, you can build proficiency in this essential skill, fostering numerical literacy and enhancing your problem-solving capabilities. Remember that consistent practice and a solid understanding of the underlying concepts are keys to success in working with percentages.
Latest Posts
Latest Posts
-
Number In Words From 1 To 100
May 14, 2025
-
What Is 96 Inches In Feet
May 14, 2025
-
What Percentage Is 35 Out Of 40
May 14, 2025
-
Electricity Is Measured In What Unit
May 14, 2025
-
Is A Pencil A Conductor Or Insulator
May 14, 2025
Related Post
Thank you for visiting our website which covers about What Is 20 Percent Of 50 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.