What Is 15 Percent Of 600
Juapaving
May 13, 2025 · 5 min read
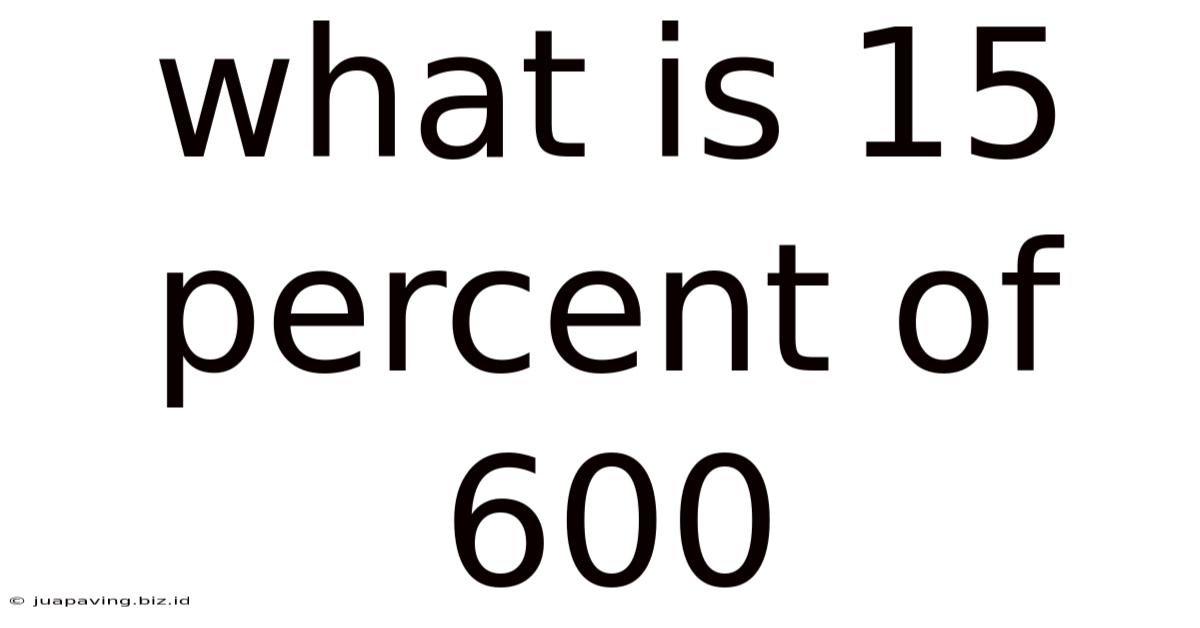
Table of Contents
What is 15 Percent of 600? A Deep Dive into Percentage Calculations
Calculating percentages is a fundamental skill in many aspects of life, from figuring out sales tax and discounts to understanding financial statements and statistical data. This article will not only answer the question "What is 15 percent of 600?" but will also explore various methods to solve this type of problem, provide practical applications, and delve into the broader concept of percentage calculations.
Understanding Percentages
A percentage is a fraction or ratio expressed as a number out of 100. The term "percent" is derived from the Latin phrase "per centum," meaning "out of a hundred." Therefore, 15 percent (15%) means 15 out of 100, or 15/100, which simplifies to 3/20 as a fraction. Understanding this basic principle is crucial to solving percentage problems.
Method 1: Using the Decimal Equivalent
This is arguably the most straightforward method. To find 15% of 600, first convert the percentage to its decimal equivalent by dividing it by 100.
15% ÷ 100 = 0.15
Next, multiply the decimal equivalent by the number you want to find the percentage of:
0.15 x 600 = 90
Therefore, 15% of 600 is $\boxed{90}$.
This method is efficient and easily adaptable to any percentage calculation. Simply convert the percentage to a decimal and multiply.
Method 2: Using Fractions
As mentioned earlier, 15% can be expressed as the fraction 15/100, which simplifies to 3/20. To find 15% of 600 using fractions, we perform the following calculation:
(3/20) x 600
We can simplify this by canceling out common factors:
(3/20) x 600 = 3 x (600/20) = 3 x 30 = 90
Again, we arrive at the answer: $\boxed{90}$. This method is particularly useful when dealing with percentages that have easily simplified fractional equivalents.
Method 3: Using Proportions
This method utilizes the concept of proportions, setting up an equation to solve for the unknown value. We can express the problem as a proportion:
15/100 = x/600
Where 'x' represents the unknown value (15% of 600). To solve for x, we cross-multiply:
15 x 600 = 100 x x
9000 = 100x
Now, divide both sides by 100:
x = 9000/100 = 90
Thus, we confirm that 15% of 600 is $\boxed{90}$. This method is helpful in understanding the underlying relationship between percentages and proportions.
Practical Applications of Percentage Calculations
Percentage calculations are ubiquitous in everyday life and across various professions. Here are some examples:
1. Sales and Discounts:
Retail stores frequently offer discounts as a percentage. For instance, a 20% discount on a $200 item can be easily calculated using the methods outlined above. This helps consumers quickly determine the final price after the discount.
2. Taxes:
Sales tax, income tax, and property tax are all expressed as percentages. Understanding percentage calculations is essential to determine the total cost of an item including tax or the amount of tax owed on income or property.
3. Financial Calculations:
Percentages are crucial in finance. Interest rates on loans and savings accounts are expressed as percentages. Understanding percentage calculations is critical for comparing different financial products and making informed decisions. Profit margins, return on investment (ROI), and many other financial metrics rely heavily on percentage calculations.
4. Statistics and Data Analysis:
Percentages are extensively used to represent data in statistics. For example, expressing survey results, demographic breakdowns, or the prevalence of a particular condition often utilizes percentages. Understanding percentages helps interpret data and draw meaningful conclusions.
5. Tip Calculations:
Calculating tips in restaurants is a common application of percentage calculations. A common tip amount is 15%, so calculating 15% of the bill is a practical use of this skill.
Advanced Percentage Calculations
While the examples above involve simple percentage calculations, the principles can be extended to more complex scenarios. These might include:
- Calculating percentage increase or decrease: This involves determining the percentage change between two values. For example, calculating the percentage increase in sales from one year to the next.
- Finding the original value after a percentage increase or decrease: This requires working backwards from the final value to determine the initial value.
- Calculating compound interest: This involves calculating interest on both the principal amount and accumulated interest.
Mastering basic percentage calculations provides a strong foundation for tackling these more advanced problems.
Common Mistakes to Avoid
Several common errors can occur when calculating percentages:
- Incorrect decimal conversion: Mistakes in converting percentages to decimals (e.g., using 15 instead of 0.15) can lead to significantly wrong results.
- Order of operations: Following the correct order of operations (multiplication before addition or subtraction) is crucial.
- Misinterpreting the question: Carefully read and understand the question to ensure you are calculating the correct percentage. For instance, the question might ask for the percentage increase, rather than just the percentage value.
Conclusion: Mastering Percentages for Success
The ability to accurately calculate percentages is a valuable skill that extends far beyond the classroom. Whether you're managing your personal finances, making business decisions, or analyzing data, a strong understanding of percentages is essential. By understanding the different methods outlined in this article and practicing regularly, you can build confidence and proficiency in this fundamental mathematical skill. Remember, practice makes perfect, and the more you engage with percentage calculations, the easier and more intuitive they will become. Mastering percentages will equip you with a powerful tool for navigating the numerical world around you.
Latest Posts
Latest Posts
-
Which Of The Following Statements Is True About
May 13, 2025
-
Why Is The Blood Testis Barrier Important
May 13, 2025
-
What Is The Strongest Type Of Intermolecular Force
May 13, 2025
-
Animals That Cannot Make Their Own Food Are Called
May 13, 2025
-
How Many Obtuse Angles Are In A Obtuse Triangle
May 13, 2025
Related Post
Thank you for visiting our website which covers about What Is 15 Percent Of 600 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.