What Is 11 Out Of 15 As A Percentage
Juapaving
May 10, 2025 · 4 min read
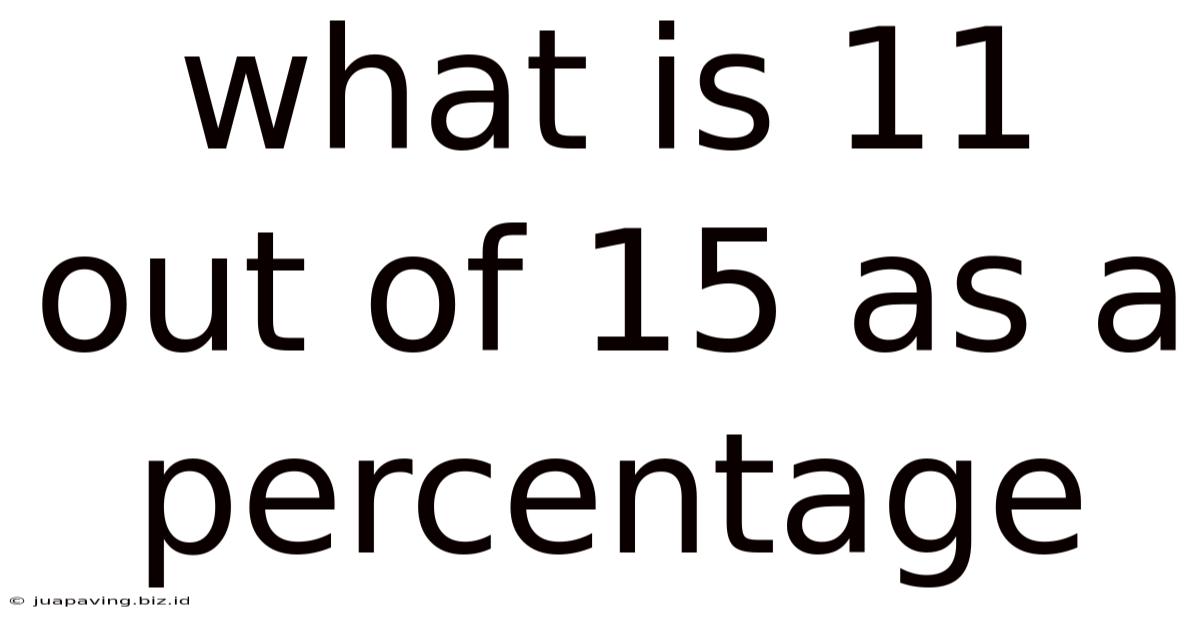
Table of Contents
What is 11 out of 15 as a Percentage? A Comprehensive Guide
Calculating percentages is a fundamental skill applicable across numerous fields, from academic studies and financial planning to everyday decision-making. Understanding how to convert fractions to percentages empowers you to interpret data, compare values, and make informed choices. This article delves into the specific calculation of "11 out of 15 as a percentage," providing a detailed explanation, various methods for calculation, and practical applications.
Understanding Fractions and Percentages
Before diving into the calculation, let's clarify the basics. A fraction represents a part of a whole. In the case of "11 out of 15," 11 represents the part, and 15 represents the whole. A percentage, denoted by the symbol %, expresses a fraction as a portion of 100. Therefore, converting "11 out of 15" to a percentage involves determining what portion of 100 11 represents when compared to 15.
Method 1: Using the Formula
The most straightforward method involves using a simple formula:
(Part / Whole) x 100% = Percentage
In this instance:
(11 / 15) x 100% = Percentage
Let's break down the calculation:
-
Division: 11 divided by 15 equals approximately 0.7333.
-
Multiplication: 0.7333 multiplied by 100 equals 73.33.
-
Result: Therefore, 11 out of 15 is approximately 73.33%.
This method provides a precise answer and is widely used for its simplicity and accuracy.
Method 2: Converting the Fraction to a Decimal
This approach involves converting the fraction to a decimal first and then multiplying by 100 to obtain the percentage.
-
Fraction to Decimal: Divide the numerator (11) by the denominator (15): 11 ÷ 15 ≈ 0.7333
-
Decimal to Percentage: Multiply the decimal by 100: 0.7333 x 100 = 73.33
-
Result: Again, the result is 73.33%. This method reinforces the understanding of decimal representation and its relation to percentages.
Method 3: Using Proportions
This method utilizes the concept of proportions to solve for the unknown percentage. We can set up a proportion:
11/15 = x/100
Where 'x' represents the percentage we're trying to find. To solve for x, we cross-multiply:
11 * 100 = 15 * x
1100 = 15x
x = 1100 / 15
x ≈ 73.33
Therefore, x ≈ 73.33%. This method emphasizes the proportional relationship between the fraction and the percentage.
Understanding the Result: 73.33%
The calculated percentage, 73.33%, signifies that 11 represents approximately 73.33% of the total value of 15. This information is crucial for various applications. For instance, if 15 represents the total number of questions on a test and you answered 11 correctly, your score would be 73.33%.
Practical Applications of Percentage Calculations
Understanding percentage calculations is vital in numerous real-world scenarios:
1. Academic Performance:
Calculating grades, analyzing test scores, and understanding class rankings often involve percentage calculations.
2. Financial Management:
Calculating interest rates, discounts, tax amounts, and profit margins heavily rely on percentage calculations.
3. Business and Sales:
Tracking sales growth, analyzing market share, and calculating profit margins are all dependent on percentage calculations.
4. Data Analysis:
Representing data in percentages facilitates comparisons and interpretations, making it easier to draw conclusions from data sets.
5. Everyday Life:
Calculating tips, discounts, and sales tax are common applications of percentage calculations in daily life.
Rounding and Precision
In many contexts, rounding the percentage to a whole number or a specific decimal place is necessary. For example, a teacher might round 73.33% to 73% for simplicity. However, in financial calculations, higher precision might be required. The level of precision depends on the context and the required accuracy.
Advanced Percentage Calculations: Finding the Part or the Whole
While this article primarily focuses on finding the percentage when the part and the whole are known, it's also useful to understand how to find the part or the whole if the percentage is given.
Finding the Part: If you know the percentage and the whole, you can find the part using the formula:
(Percentage/100) * Whole = Part
Finding the Whole: If you know the percentage and the part, you can find the whole using the formula:
Part / (Percentage/100) = Whole
Conclusion: Mastering Percentage Calculations
The ability to calculate percentages efficiently and accurately is an essential skill. Understanding the different methods, such as using formulas, converting to decimals, or employing proportions, allows for flexibility and a deeper comprehension of the underlying concepts. The calculation of "11 out of 15 as a percentage," resulting in approximately 73.33%, demonstrates a practical application of these techniques. By mastering percentage calculations, you enhance your ability to analyze data, make informed decisions, and confidently navigate various aspects of life, from academic pursuits to professional endeavors. Remember to always consider the context and the required precision when rounding your results. The more you practice, the more comfortable and proficient you will become in tackling percentage-related problems.
Latest Posts
Latest Posts
-
Five Letter Word Starting With Be
May 10, 2025
-
This Hormone Stimulates Leydig Cells To Secrete Testosterone
May 10, 2025
-
Least Common Multiple Of 18 And 32
May 10, 2025
-
1000 Meters Equals How Many Kilometers
May 10, 2025
-
Of The Following Which Is The Strongest Base
May 10, 2025
Related Post
Thank you for visiting our website which covers about What Is 11 Out Of 15 As A Percentage . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.