What Is 1 3 Of 75000
Juapaving
May 13, 2025 · 4 min read
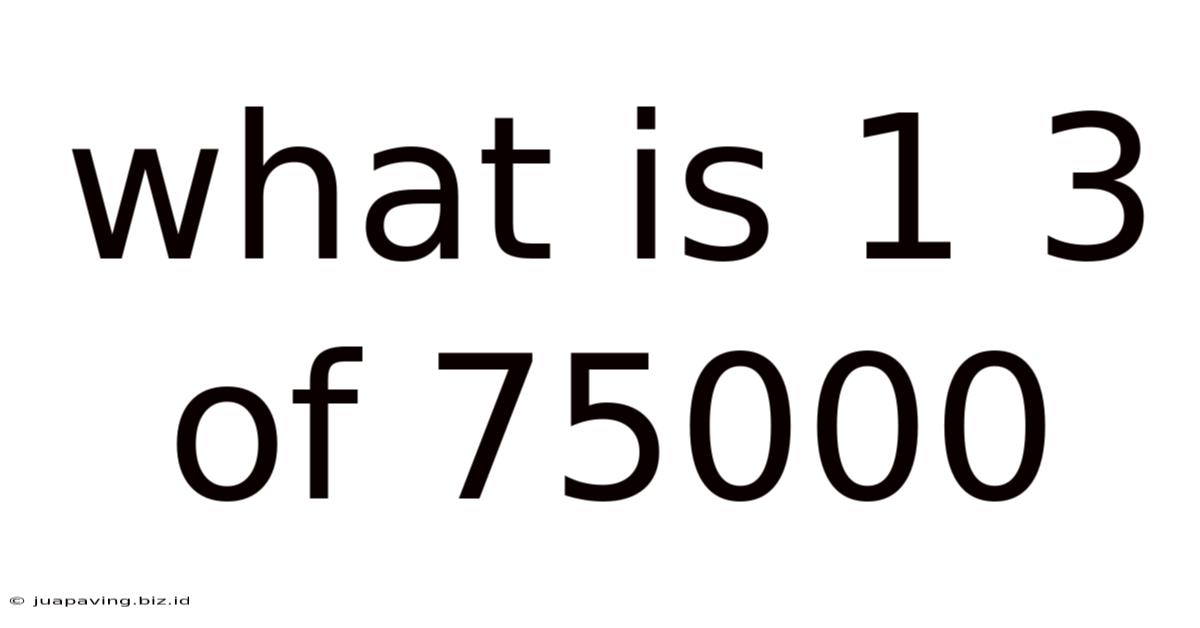
Table of Contents
What is 1/3 of 75,000? A Comprehensive Guide to Fractions and their Applications
Finding a fraction of a number is a fundamental mathematical operation with widespread applications in various fields. This article will comprehensively address the question "What is 1/3 of 75,000?" We'll explore the solution step-by-step, discuss different methods for solving similar problems, and delve into real-world examples where understanding fractions is crucial.
Understanding Fractions
Before diving into the calculation, let's refresh our understanding of fractions. A fraction represents a part of a whole. It consists of two numbers:
- Numerator: The top number, indicating the number of parts we're considering.
- Denominator: The bottom number, indicating the total number of equal parts the whole is divided into.
In our case, we have the fraction 1/3. This means we're interested in one part out of three equal parts.
Calculating 1/3 of 75,000
There are several ways to calculate 1/3 of 75,000:
Method 1: Division
The most straightforward method is to divide 75,000 by the denominator (3) and then multiply the result by the numerator (1).
1. Divide 75,000 by 3:
75,000 / 3 = 25,000
2. Multiply the result by 1 (the numerator):
25,000 * 1 = 25,000
Therefore, 1/3 of 75,000 is 25,000.
Method 2: Simplifying the Fraction (if applicable)
While not necessary in this specific case, this method is helpful when dealing with more complex fractions. If the fraction can be simplified, doing so before the calculation can make the process easier. For instance, if we were calculating 2/6 of 75,000, we would first simplify 2/6 to 1/3, and then proceed as in Method 1.
Method 3: Using Decimals
We can convert the fraction 1/3 into a decimal by performing the division:
1 / 3 ≈ 0.3333...
Then, multiply this decimal by 75,000:
0.3333... * 75,000 ≈ 25,000
This method might introduce a slight rounding error depending on the number of decimal places used, but in this case, it yields the correct result. It's crucial to be aware of potential rounding errors when using this approach.
Real-World Applications of Fractional Calculations
Understanding fractions is vital in various real-world scenarios:
1. Finance and Budgeting
- Calculating discounts: If a store offers a 1/3 discount on an item costing $75,000, the discount amount would be $25,000.
- Sharing profits: If three business partners agree to share profits equally, each partner would receive 1/3 of the total profit.
- Investment returns: Calculating returns on investments often involves fractions.
2. Measurement and Engineering
- Scaling blueprints: Architects and engineers frequently use fractions to scale blueprints. A 1/3 scale means that 1 unit on the blueprint represents 3 units in reality.
- Calculating quantities: Construction projects involve calculations with fractions to determine precise quantities of materials needed.
3. Cooking and Baking
- Scaling recipes: Recipes often need to be scaled up or down, requiring fractional calculations. If a recipe calls for 1/3 cup of sugar, and you want to double the recipe, you'll need 2/3 cup of sugar.
4. Data Analysis and Statistics
- Calculating proportions: Fractions are crucial in representing and analyzing proportions in data sets. For example, determining the proportion of a population that prefers a particular product.
- Probability: Probability calculations often involve fractions. For instance, the probability of an event occurring might be expressed as a fraction.
Expanding on Fraction Calculations: Dealing with More Complex Scenarios
While this article focused on calculating 1/3 of 75,000, the principles discussed can be applied to more complex scenarios. Let's consider some variations:
-
Calculating a different fraction: If you need to find, say, 2/5 of 75,000, you would divide 75,000 by 5 (the denominator) and then multiply by 2 (the numerator). This would give you 30,000.
-
Dealing with mixed numbers: A mixed number combines a whole number and a fraction (e.g., 2 1/3). To calculate with mixed numbers, first convert them to improper fractions (e.g., 7/3 for 2 1/3). Then, proceed with the same division and multiplication process.
-
Calculating percentages: Percentages are essentially fractions with a denominator of 100. For example, 33.33% is equivalent to 1/3. You can calculate percentages using the same methods described above.
Conclusion: Mastering Fractions for Everyday Life
Understanding fractions is a fundamental skill applicable across a wide range of fields. This article demonstrated how to efficiently calculate 1/3 of 75,000 using different approaches, highlighting the simplicity and practicality of these methods. By mastering these techniques, you can confidently tackle numerous real-world problems involving fractions and improve your problem-solving capabilities in various aspects of life. The ability to work with fractions is a valuable asset, empowering you to tackle complex problems with clarity and precision. Remember to practice regularly to solidify your understanding and build proficiency in this essential mathematical concept. From financial planning to engineering projects, the application of fraction calculations is pervasive and impactful.
Latest Posts
Latest Posts
-
Which Is Longer An Inch Or A Centimeter
May 13, 2025
-
1 Ton Is How Many Kg
May 13, 2025
-
What Gas Do Plants Absorb From The Atmosphere
May 13, 2025
-
Which Of The Following Statement Is Accurate
May 13, 2025
-
If Lines Are Parallel Then Alternate Interior Angles Are
May 13, 2025
Related Post
Thank you for visiting our website which covers about What Is 1 3 Of 75000 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.