What Fraction Is Equal To 4 5
Juapaving
May 13, 2025 · 5 min read
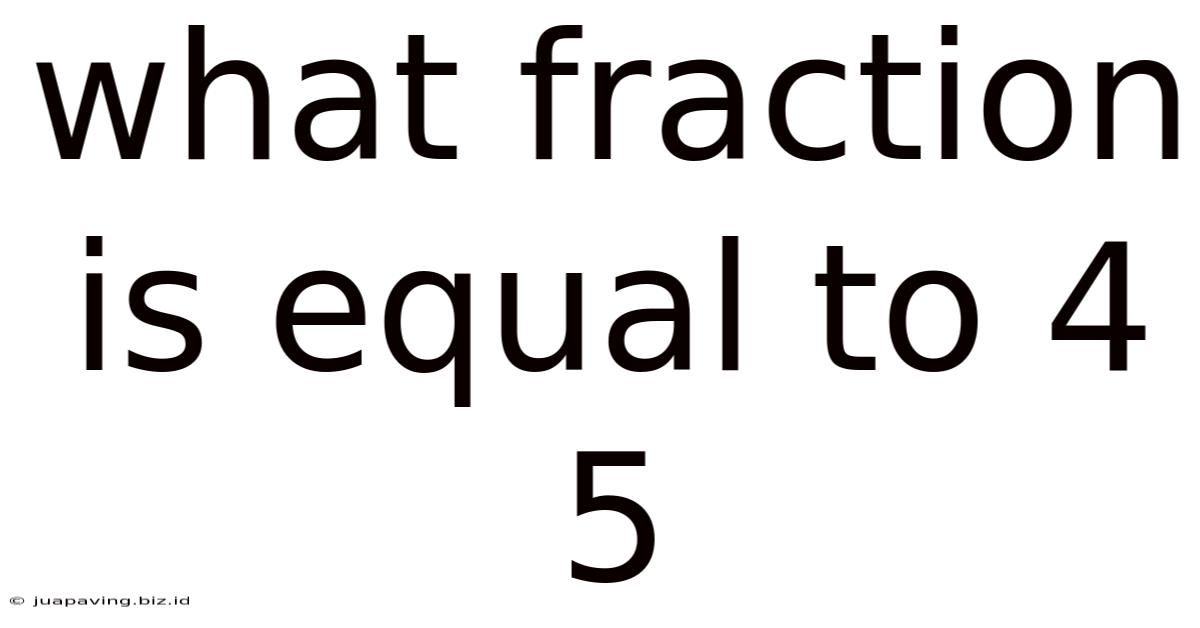
Table of Contents
What Fraction is Equal to 4/5? A Deep Dive into Fractions and Their Equivalents
Understanding fractions is fundamental to mathematics and numerous real-world applications. This comprehensive guide explores the fraction 4/5, delving into its meaning, equivalent fractions, decimal representation, percentage equivalent, and practical examples to solidify your understanding. We'll also touch upon the broader concepts of simplifying fractions and finding equivalent fractions to build a strong foundation in this area of mathematics.
Understanding the Fraction 4/5
The fraction 4/5 represents a part of a whole. It's composed of two key components:
- Numerator (4): This number indicates the number of parts we're considering.
- Denominator (5): This number shows the total number of equal parts the whole is divided into.
Therefore, 4/5 signifies that we have 4 out of 5 equal parts of a whole. Imagine a pizza cut into 5 equal slices; 4/5 represents having 4 of those slices.
Finding Equivalent Fractions to 4/5
Equivalent fractions represent the same value even though they look different. They are created by multiplying or dividing both the numerator and the denominator by the same non-zero number. This process doesn't change the fundamental ratio between the numerator and the denominator.
Let's find some equivalent fractions for 4/5:
- Multiplying by 2: (4 x 2) / (5 x 2) = 8/10
- Multiplying by 3: (4 x 3) / (5 x 3) = 12/15
- Multiplying by 4: (4 x 4) / (5 x 4) = 16/20
- Multiplying by 5: (4 x 5) / (5 x 5) = 20/25
- Multiplying by 10: (4 x 10) / (5 x 10) = 40/50
And so on. You can generate an infinite number of equivalent fractions for 4/5 by multiplying both the numerator and the denominator by any non-zero integer.
Conversely, if you have a fraction like 20/25 and you want to simplify it, you would find the greatest common divisor (GCD) of the numerator and the denominator, which is 5 in this case, and then divide both by 5. This leads you back to 4/5, demonstrating the relationship between equivalent fractions.
Importance of Equivalent Fractions
Understanding equivalent fractions is crucial for several reasons:
- Simplifying fractions: Reducing a fraction to its simplest form (where the numerator and denominator share no common factors other than 1) makes it easier to work with.
- Comparing fractions: To compare fractions effectively, you often need to find equivalent fractions with a common denominator.
- Solving equations: Many algebraic equations involving fractions require finding equivalent fractions to simplify the process.
- Real-world applications: In situations involving proportions and ratios, equivalent fractions play a significant role in problem-solving. For instance, scaling recipes or determining the proportion of ingredients in a mixture often involves working with equivalent fractions.
Decimal Representation of 4/5
To convert a fraction to a decimal, simply divide the numerator by the denominator:
4 ÷ 5 = 0.8
Therefore, the decimal representation of 4/5 is 0.8. This decimal is a terminating decimal, meaning it has a finite number of digits after the decimal point. Not all fractions result in terminating decimals; some produce repeating decimals (like 1/3 = 0.333...).
Percentage Equivalent of 4/5
To convert a fraction to a percentage, first convert it to a decimal (as shown above), then multiply by 100 and add the "%" symbol:
0.8 x 100% = 80%
Therefore, 4/5 is equivalent to 80%. This means that 4/5 represents 80 parts out of 100 equal parts.
Practical Applications of 4/5
The fraction 4/5, or its equivalents (8/10, 80%, 0.8), appears frequently in various real-world scenarios:
- Discounts: A store offering an 80% discount means you're paying only 20% of the original price (which is equivalent to 1/5).
- Surveys and polls: If 80% of respondents agree with a particular statement in a survey, this represents 4/5 of the total respondents.
- Measurements: If a container is 4/5 full, it means that 80% of its capacity is filled.
- Recipe scaling: When doubling or halving a recipe, you might need to work with fractions and their equivalents to adjust the quantities of ingredients accurately. For example, if a recipe calls for 4/5 cup of flour, doubling it would require 8/5 cups or 1 3/5 cups of flour.
- Financial calculations: Interest rates, profit margins, and many other financial calculations involve fractions and their decimal or percentage equivalents.
Simplifying Fractions: A General Approach
Simplifying fractions, also known as reducing fractions to their lowest terms, involves finding the greatest common divisor (GCD) of the numerator and the denominator and dividing both by the GCD. The GCD is the largest number that divides both the numerator and the denominator without leaving a remainder.
For instance, consider the fraction 12/18:
-
Find the GCD of 12 and 18: The factors of 12 are 1, 2, 3, 4, 6, and 12. The factors of 18 are 1, 2, 3, 6, 9, and 18. The greatest common factor is 6.
-
Divide both the numerator and the denominator by the GCD: 12 ÷ 6 = 2 and 18 ÷ 6 = 3.
-
Simplified fraction: The simplified fraction is 2/3.
There are various methods to find the GCD, including the Euclidean algorithm, which is particularly useful for larger numbers.
Finding Equivalent Fractions: A Step-by-Step Guide
To find equivalent fractions, follow these steps:
-
Choose a multiplier: Select any non-zero integer as your multiplier.
-
Multiply the numerator: Multiply the original numerator by the chosen multiplier.
-
Multiply the denominator: Multiply the original denominator by the same multiplier.
-
New equivalent fraction: The resulting fraction is an equivalent fraction of the original fraction.
For example, let's find an equivalent fraction for 3/4 using a multiplier of 5:
-
Multiplier: 5
-
Multiply the numerator: 3 x 5 = 15
-
Multiply the denominator: 4 x 5 = 20
-
Equivalent fraction: 15/20 is an equivalent fraction to 3/4.
Conclusion: Mastering Fractions for Real-World Success
Understanding fractions, including finding equivalent fractions and simplifying fractions, is a cornerstone of mathematical literacy. The fraction 4/5, with its various representations (0.8, 80%), holds significant relevance in countless daily situations, from financial calculations to recipe adjustments. By grasping the concepts discussed here, you'll be better equipped to handle fraction-related problems efficiently and confidently, enhancing your problem-solving abilities in various aspects of life. Remember, practice is key to mastering fractions and building a solid foundation in mathematical understanding.
Latest Posts
Latest Posts
-
2 Hours And 20 Minutes In Minutes
May 13, 2025
-
How To Find Ions In A Compound
May 13, 2025
-
Lines In The Same Plane That Never Intersect
May 13, 2025
-
16 5 As A Mixed Number
May 13, 2025
-
Is Brass An Element Compound Or Mixture
May 13, 2025
Related Post
Thank you for visiting our website which covers about What Fraction Is Equal To 4 5 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.