What Does Line Mean In Math
Juapaving
Apr 02, 2025 · 6 min read
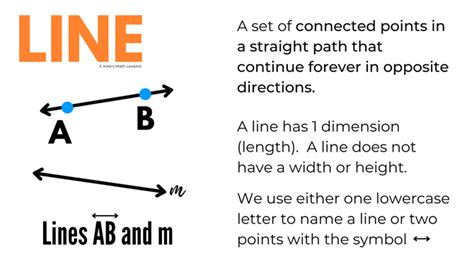
Table of Contents
What Does Line Mean in Math? A Comprehensive Guide
The seemingly simple concept of a "line" in mathematics holds far more depth than initially meets the eye. While intuitively, we understand a line as a continuous, straight mark, its mathematical definition and properties extend significantly, forming the foundation for numerous advanced concepts in geometry, algebra, and calculus. This comprehensive guide explores the multifaceted meaning of a line in mathematics, covering its various representations, properties, equations, and applications.
Defining a Line: The Fundamental Concepts
At its core, a line in mathematics is a one-dimensional geometric object that extends infinitely in both directions. This "infinite extension" is a crucial aspect differentiating it from a line segment (a finite portion of a line) or a ray (a half-line starting at a point and extending infinitely in one direction). A line possesses no thickness or width; it's purely a collection of points arranged in a perfectly straight manner.
Key Characteristics of a Line:
- Straightness: A line always follows a perfectly straight path; it never curves or bends.
- Infinite Extension: It extends indefinitely in both directions, without any end points.
- One-dimensionality: It only possesses length; it has no width or depth.
- Defined by Two Points: A unique line can always be defined by any two distinct points lying on it.
Representing Lines: Different Notations and Methods
Mathematicians employ several methods to represent lines, each offering unique advantages depending on the context:
1. Geometric Representation:
This is the most intuitive approach. Lines are visually represented as straight lines using a ruler or drawing tools. Labels or letters (e.g., line l, line AB) are often used to identify specific lines in diagrams or illustrations.
2. Algebraic Representation:
This method utilizes equations to precisely define the location and orientation of a line within a coordinate system. The most common representations are:
-
Slope-Intercept Form:
y = mx + bwhere m represents the slope (steepness) of the line and b represents the y-intercept (the point where the line crosses the y-axis). This form is particularly useful when the slope and y-intercept are known. -
Point-Slope Form:
y - y₁ = m(x - x₁)where m is the slope and (x₁, y₁) is a known point on the line. This form is convenient when the slope and a point on the line are given. -
Standard Form:
Ax + By = Cwhere A, B, and C are constants. While less intuitive, this form is useful for various algebraic manipulations and finding intercepts. -
Two-Point Form:
(y - y₁) / (x - x₁) = (y₂ - y₁) / (x₂ - x₁)where (x₁, y₁) and (x₂, y₂) are two distinct points on the line. This is useful when only two points are known.
3. Vector Representation:
In vector geometry, a line can be defined using a vector equation:
r = a + λbwhere r is a position vector on the line, a is the position vector of a point on the line, b is a direction vector parallel to the line, and λ is a scalar parameter. This representation is powerful for describing lines in higher dimensions and facilitates various geometric operations.
Properties of Lines: Parallelism, Perpendicularity, and Intersection
Lines exhibit several key properties influencing their relationships with other lines and geometric figures:
1. Parallel Lines:
Two or more lines are parallel if they lie in the same plane and never intersect, no matter how far they are extended. In algebraic terms, parallel lines have the same slope (in the slope-intercept form).
2. Perpendicular Lines:
Two lines are perpendicular if they intersect at a right angle (90 degrees). Algebraically, the slopes of perpendicular lines are negative reciprocals of each other (if one slope is m, the other is -1/m).
3. Intersecting Lines:
Lines that are not parallel intersect at exactly one point. The coordinates of this intersection point can be found by solving the system of equations representing the lines.
Lines in Different Geometries: Expanding the Scope
The concept of a line extends beyond Euclidean geometry, adapting to the unique properties of other geometrical systems:
1. Euclidean Geometry:
This is the most familiar geometry, where lines are straight, parallel lines remain equidistant, and the angles of a triangle sum to 180 degrees.
2. Non-Euclidean Geometries:
In geometries like hyperbolic or elliptic geometry, the properties of lines deviate from those of Euclidean geometry. For example, parallel lines might not exist, or the angles of a triangle might sum to more or less than 180 degrees. The definition of a "line" remains central, but its characteristics are adjusted according to the axioms of the specific non-Euclidean system.
3. Projective Geometry:
Projective geometry extends Euclidean geometry by incorporating ideal points (points at infinity), which allows parallel lines to intersect at a point at infinity. This seemingly paradoxical concept simplifies various geometric transformations and constructions.
Applications of Lines in Mathematics and Beyond:
Lines are fundamental building blocks in numerous mathematical concepts and have widespread applications in various fields:
1. Linear Algebra:
Lines form the basis of vector spaces, linear transformations, and matrix operations. Understanding linear equations and their geometric representations is crucial for solving systems of linear equations and analyzing linear systems.
2. Calculus:
Lines are used to approximate curves using tangents (lines that touch a curve at a single point and share the same slope at that point), and secants (lines intersecting a curve at two points). The concept of the derivative, a central concept in calculus, is inherently linked to the slope of a tangent line.
3. Geometry:
Lines are essential for defining geometric shapes, angles, and relationships between points and figures. Concepts like collinearity (points lying on the same line), concurrency (lines intersecting at the same point), and various geometric constructions heavily rely on lines.
4. Computer Graphics and Computer-Aided Design (CAD):
Lines are the fundamental elements used to create images and models in computer graphics and CAD software. Representing objects as collections of lines and curves allows for efficient rendering, manipulation, and analysis of designs.
5. Physics and Engineering:
Lines are used to represent trajectories of objects, directions of forces, and various physical phenomena. In engineering, lines are used to model structures, paths of vehicles, and various other applications.
Conclusion: The Enduring Importance of Lines in Mathematics
The concept of a line, while seemingly basic, plays a crucial and multifaceted role in mathematics. Its simple definition belies the profound implications it carries in numerous branches of mathematics and its applications in diverse fields. From defining geometric shapes to representing complex mathematical relationships, the line serves as a fundamental building block for understanding and modeling our world. This article has provided a comprehensive overview of the various aspects of lines in mathematics, but further exploration into specific branches like linear algebra, differential geometry, or projective geometry will reveal even more intricate details and applications of this foundational mathematical object.
Latest Posts
Latest Posts
-
Least Common Multiple Of 15 And 18
Apr 03, 2025
-
Do Both Plant And Animal Cells Have Plasma Membrane
Apr 03, 2025
-
Black Soil Is Also Known As
Apr 03, 2025
-
Words With Ed At The End
Apr 03, 2025
-
96 Inches Is How Many Feet
Apr 03, 2025
Related Post
Thank you for visiting our website which covers about What Does Line Mean In Math . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
