What Do I Multiply Do Get 216
Juapaving
Apr 04, 2025 · 4 min read
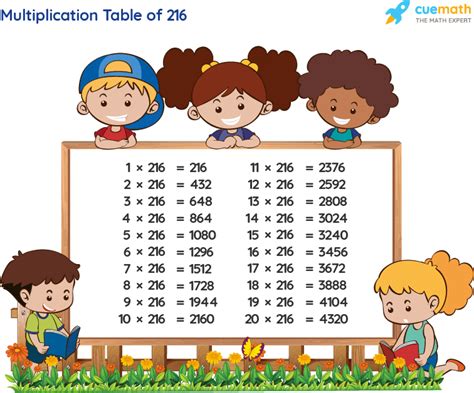
Table of Contents
What Do I Multiply to Get 216? A Deep Dive into Factorization
Finding the numbers that multiply to equal 216 might seem like a simple math problem, but it opens the door to a fascinating exploration of factors, prime factorization, and the broader world of number theory. This comprehensive guide will not only answer the question "What do I multiply to get 216?" but also equip you with the tools and understanding to tackle similar problems with ease.
Understanding Factors and Multiples
Before diving into the specifics of 216, let's establish a fundamental understanding of factors and multiples.
Factors: Factors are numbers that divide evenly into another number without leaving a remainder. For example, the factors of 12 are 1, 2, 3, 4, 6, and 12. Each of these numbers divides perfectly into 12.
Multiples: Multiples are the result of multiplying a number by any integer. For example, multiples of 3 are 3, 6, 9, 12, 15, and so on.
Finding the Factors of 216: A Step-by-Step Approach
There are several ways to find the factors of 216. Here are a few effective methods:
1. Trial and Error:
This method involves systematically testing numbers to see if they divide evenly into 216. Start with 1 and work your way up.
- 1 x 216 = 216
- 2 x 108 = 216
- 3 x 72 = 216
- 4 x 54 = 216
- 6 x 36 = 216
- 8 x 27 = 216
- 9 x 24 = 216
- 12 x 18 = 216
This method is straightforward but can become time-consuming for larger numbers.
2. Prime Factorization:
This is a more efficient and elegant approach. Prime factorization breaks a number down into its prime factors – numbers that are only divisible by 1 and themselves (e.g., 2, 3, 5, 7, 11...).
Let's find the prime factorization of 216:
- Start with the smallest prime number, 2: 216 is even, so it's divisible by 2. 216 ÷ 2 = 108
- Continue dividing by 2: 108 is also even. 108 ÷ 2 = 54. And again: 54 ÷ 2 = 27
- Move to the next prime number, 3: 27 is divisible by 3. 27 ÷ 3 = 9. And again: 9 ÷ 3 = 3. Finally: 3 ÷ 3 = 1
Therefore, the prime factorization of 216 is 2 x 2 x 2 x 3 x 3 x 3, or 2³ x 3³.
This prime factorization provides a complete set of factors. Any combination of these prime factors, multiplied together, will yield a factor of 216.
3. Factor Tree:
A factor tree is a visual representation of the prime factorization process. It's a helpful tool, especially for larger numbers. Here's a factor tree for 216:
216
/ \
2 108
/ \
2 54
/ \
2 27
/ \
3 9
/ \
3 3
Reading the bottom branches gives us the prime factors: 2 x 2 x 2 x 3 x 3 x 3 = 216.
All Possible Pairs of Factors for 216
Using the prime factorization and trial and error methods, we can list all the pairs of numbers that multiply to 216:
- 1 x 216
- 2 x 108
- 3 x 72
- 4 x 54
- 6 x 36
- 8 x 27
- 9 x 24
- 12 x 18
Beyond Pairs: Exploring Combinations
While pairs of numbers are commonly sought, remember that you can also use more than two numbers to multiply to 216. For example:
- 2 x 2 x 2 x 27 = 216
- 2 x 3 x 36 = 216
- 2 x 2 x 3 x 18 = 216
- 2 x 2 x 9 x 6 = 216
- And many other possibilities!
Applying This Knowledge: Real-World Examples
Understanding factors and multiples extends far beyond simple arithmetic. It's crucial in various areas, such as:
- Geometry: Calculating areas and volumes frequently involves finding factors.
- Data analysis: Grouping data into equal sets often requires factoring.
- Computer science: Algorithms and data structures frequently utilize factorization concepts.
- Cryptography: Prime factorization is at the heart of many encryption methods.
Expanding Your Skills: Working with Larger Numbers
The techniques described above are applicable to larger numbers as well. While the trial-and-error method becomes less practical for very large numbers, prime factorization remains efficient. For extremely large numbers, advanced algorithms are employed.
Conclusion: Mastering Multiplication and Factorization
Learning to identify the numbers that multiply to 216, and more importantly, understanding the underlying principles of factorization, is a valuable skill that builds a stronger mathematical foundation. This knowledge extends beyond simple arithmetic, opening up opportunities for deeper explorations in various fields. Whether you're a student, a professional, or simply someone curious about numbers, mastering factorization techniques will significantly enhance your mathematical abilities and problem-solving skills. Remember to practice regularly, explore different methods, and challenge yourself with progressively larger numbers to solidify your understanding. The world of numbers is vast and fascinating—enjoy the journey of discovery!
Latest Posts
Latest Posts
-
Five Letter Words Ending In O N
Apr 04, 2025
-
What Is Keratinization And Where Does It Occur
Apr 04, 2025
-
Drawing Of The Reaction Of Hydrochloric Acid With Water
Apr 04, 2025
-
How Many Feet Are In 41 Inches
Apr 04, 2025
-
Glycogen Is The Storage Form Of Glucose In Plants
Apr 04, 2025
Related Post
Thank you for visiting our website which covers about What Do I Multiply Do Get 216 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
