What Divided By What Equals Pi
Juapaving
May 11, 2025 · 6 min read
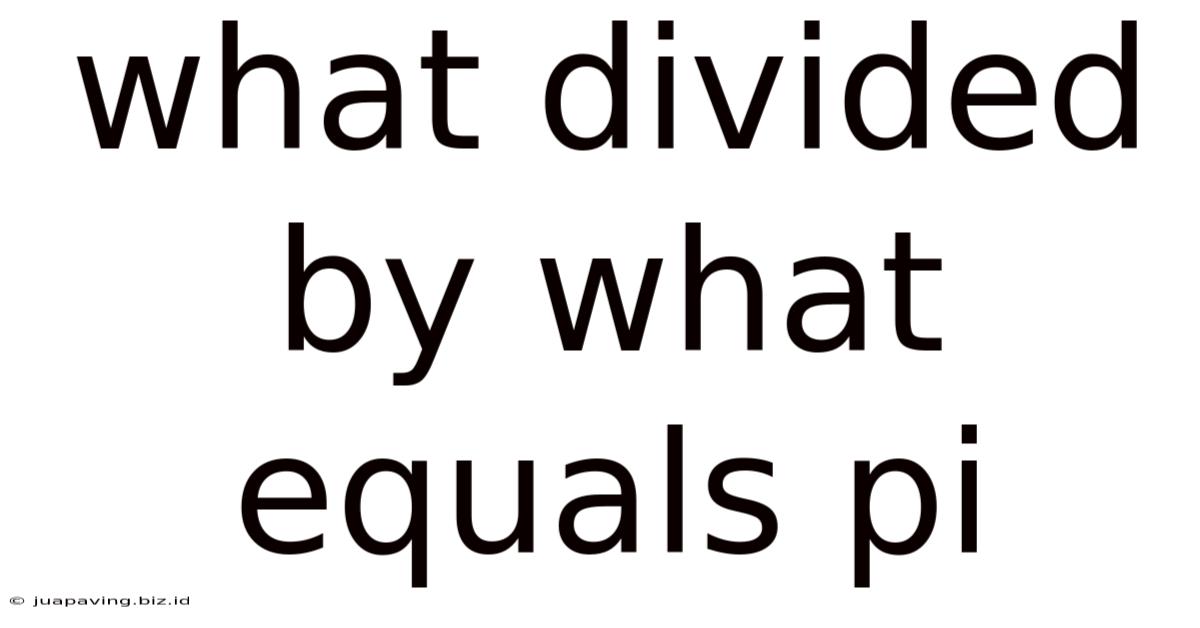
Table of Contents
What Divided by What Equals Pi? Exploring the Mathematical Mysteries of π
Pi (π), approximately equal to 3.14159, is a fundamental mathematical constant representing the ratio of a circle's circumference to its diameter. While its value is readily available, the question of "what divided by what equals pi?" delves into a deeper understanding of its mathematical properties and reveals surprising connections across different areas of mathematics. This article explores various approaches to conceptualizing this ratio, moving beyond simple approximations and delving into the intricacies of infinite series, calculus, and probability.
The Fundamental Definition: Circumference and Diameter
The most straightforward answer to the question is: a circle's circumference divided by its diameter equals pi. This is the very definition of pi. This seemingly simple statement holds profound implications, forming the foundation for countless mathematical formulas and applications in geometry, trigonometry, and beyond.
Understanding the Ratio
Imagine a circle of any size. Measure its circumference (the distance around the circle) and its diameter (the distance across the circle through the center). No matter the size of the circle, the ratio of the circumference to the diameter will always be approximately 3.14159... This consistent ratio is what we define as π.
Limitations of Measurement
While this definition is conceptually clear, practically obtaining a perfectly accurate measurement of a circle's circumference and diameter is impossible. Real-world measurements are always subject to error. This is why pi is represented as an irrational number – its decimal representation goes on forever without repeating.
Approximating Pi: From Ancient Civilizations to Modern Algorithms
Approximating pi has been a pursuit for millennia. Ancient civilizations used various methods, often yielding surprisingly accurate estimations.
Early Approximations
The Babylonians approximated pi as 3.125, while the Egyptians used a value close to 3.16. These approximations, though imprecise compared to modern calculations, demonstrate humanity's early attempts to grasp the nature of this fundamental constant.
The Archimedes Method
Archimedes, a renowned ancient Greek mathematician, developed a method using inscribed and circumscribed polygons to approximate pi. By progressively increasing the number of sides of these polygons, he refined the approximation, achieving a remarkable level of accuracy for his time. This approach exemplifies the early application of iterative methods in approximating pi.
Infinite Series and Calculus
The development of calculus provided a powerful new tool for calculating pi. Gottfried Wilhelm Leibniz discovered the Leibniz formula for π, an infinite series that can be used to calculate pi:
π/4 = 1 - 1/3 + 1/5 - 1/7 + 1/9 - ...
This formula, though elegant, converges to pi very slowly, requiring a vast number of terms for reasonable accuracy. Other more efficient infinite series, like the Ramanujan formula, offer faster convergence, allowing for the computation of pi to millions or even trillions of digits.
Monte Carlo Methods
Interestingly, pi can also be approximated using probabilistic methods, such as the Monte Carlo method. Imagine throwing darts randomly at a square with a circle inscribed within it. The ratio of the number of darts landing within the circle to the total number of darts thrown provides an approximation of pi. This seemingly unrelated approach highlights the surprising connections between geometry and probability.
Beyond the Basic Definition: Pi in Different Mathematical Contexts
Pi's significance extends far beyond the simple ratio of a circle's circumference to its diameter. It appears in numerous and unexpected mathematical contexts:
Trigonometry and Oscillatory Phenomena
Pi plays a crucial role in trigonometry, particularly in the definitions of trigonometric functions like sine, cosine, and tangent. These functions, which describe periodic or oscillatory phenomena, are fundamental in fields like physics and engineering. The value of pi dictates the period of these functions, reflecting the cyclical nature of waves and oscillations.
Calculus and Infinite Series
As discussed earlier, pi is intricately linked to calculus and infinite series. Many important formulas in calculus, particularly those involving integrals and derivatives, incorporate pi, demonstrating its fundamental role in the field. The calculation of areas, volumes, and arc lengths often involve pi as a constant of proportionality.
Probability and Statistics
The appearance of pi in probability and statistics might seem surprising, but it reflects the underlying mathematical connections. For example, in the calculation of the normal distribution curve (the bell curve), pi appears in the normalization constant, influencing the shape and spread of this widely used statistical distribution.
Complex Numbers and Euler's Identity
One of the most beautiful and unexpected appearances of pi occurs in Euler's identity:
e^(iπ) + 1 = 0
This identity connects five fundamental mathematical constants – e (Euler's number), i (the imaginary unit), π, 1, and 0 – in a surprisingly elegant equation. This equation is considered one of the most beautiful equations in mathematics, showcasing the interconnectedness of seemingly disparate mathematical concepts.
The Ongoing Quest for Pi
Despite millennia of study, the quest for a deeper understanding of pi continues. Researchers are constantly seeking more efficient algorithms for calculating pi to trillions of digits, primarily driven by testing the limits of computational power and exploring potential patterns within the seemingly random digits. The pursuit is not merely about obtaining more digits, but about refining computational techniques and advancing our understanding of the fundamental nature of this constant.
Pi's Applications in the Real World
Pi's theoretical elegance translates to countless practical applications across diverse fields. Here are some examples:
Engineering and Physics
Pi is essential in engineering calculations involving circles, cylinders, and spheres. From designing bridges and buildings to constructing pipelines and aerospace components, accurate pi calculations are critical for ensuring structural integrity and functionality. In physics, pi appears in formulas related to wave propagation, oscillations, and gravitational forces, highlighting its relevance in understanding natural phenomena.
Computer Science and Algorithm Design
The calculation of pi is often used as a benchmark for testing computer performance and the efficiency of algorithms. The pursuit of faster and more accurate pi calculations drives advancements in computational power and algorithm design.
Statistics and Data Analysis
Pi's role in statistical distributions, as mentioned earlier, has significant implications for data analysis and modelling. Understanding the normal distribution, which incorporates pi, is crucial for analyzing data sets and making inferences.
Everyday Life
While we might not explicitly use pi in our daily calculations, it implicitly underpins numerous technologies and processes we use every day. For instance, the GPS system that guides our navigation relies on spherical trigonometry and calculations involving pi. The design of circular objects, from wheels to clocks, all involve pi in their specifications.
Conclusion: The Enduring Mystery of Pi
The question "what divided by what equals pi?" leads us on a journey through the fascinating history and multifaceted nature of this mathematical constant. While the fundamental definition is straightforward, the exploration of pi's appearances across different mathematical fields reveals its depth and significance. The ongoing quest for a deeper understanding of pi continues to inspire mathematical research, drive technological advancements, and underscore the elegance and interconnectedness of mathematics. Pi, a seemingly simple ratio, encapsulates a vast realm of mathematical knowledge and its profound impact on our world.
Latest Posts
Latest Posts
-
How Many Centimeters Are In 18 Meters
May 11, 2025
-
Give One Example Of A Chemical Change
May 11, 2025
-
Chemical Formula For Potassium And Fluorine
May 11, 2025
-
Difference Between A Characteristic And A Trait
May 11, 2025
-
What Living Things Live In The Desert
May 11, 2025
Related Post
Thank you for visiting our website which covers about What Divided By What Equals Pi . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.