What Are The Factors For 10
Juapaving
Apr 03, 2025 · 5 min read
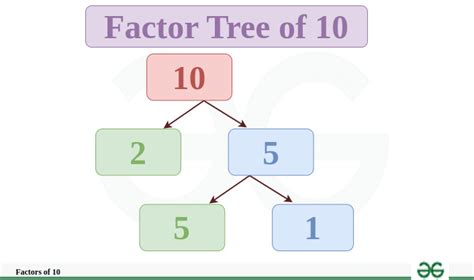
Table of Contents
What Are the Factors for 10? A Deep Dive into Number Theory and its Applications
The seemingly simple question, "What are the factors of 10?" opens a door to a fascinating world of number theory, impacting areas from cryptography to computer science. While the immediate answer is straightforward – 1, 2, 5, and 10 – a deeper exploration reveals underlying principles and practical applications far exceeding this basic calculation.
Understanding Factors and Divisibility
Before diving into the specifics of 10, let's establish a firm understanding of fundamental concepts:
What is a Factor? A factor (or divisor) of a number is any integer that divides the number without leaving a remainder. In simpler terms, it's a number that can be multiplied by another integer to produce the original number.
What is Divisibility? Divisibility refers to the ability of one number to be divided evenly by another. If a number 'a' is divisible by a number 'b', then the remainder is zero when 'a' is divided by 'b'.
Finding Factors of 10: A Simple Approach
To find the factors of 10, we can systematically check each integer from 1 up to 10:
- 1: 10 ÷ 1 = 10 (remainder 0) – Therefore, 1 is a factor.
- 2: 10 ÷ 2 = 5 (remainder 0) – Therefore, 2 is a factor.
- 3: 10 ÷ 3 = 3 with a remainder of 1 – Therefore, 3 is not a factor.
- 4: 10 ÷ 4 = 2 with a remainder of 2 – Therefore, 4 is not a factor.
- 5: 10 ÷ 5 = 2 (remainder 0) – Therefore, 5 is a factor.
- 6: 10 ÷ 6 = 1 with a remainder of 4 – Therefore, 6 is not a factor.
- 7: 10 ÷ 7 = 1 with a remainder of 3 – Therefore, 7 is not a factor.
- 8: 10 ÷ 8 = 1 with a remainder of 2 – Therefore, 8 is not a factor.
- 9: 10 ÷ 9 = 1 with a remainder of 1 – Therefore, 9 is not a factor.
- 10: 10 ÷ 10 = 1 (remainder 0) – Therefore, 10 is a factor.
This method confirms that the factors of 10 are 1, 2, 5, and 10.
Prime Factorization: Unveiling the Building Blocks
The concept of prime factorization is crucial in understanding the composition of numbers. A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. Prime factorization expresses a number as a product of its prime factors.
For 10, the prime factorization is 2 x 5. This means 10 is composed of the prime numbers 2 and 5. This simple factorization is highly significant in various mathematical operations and applications.
The Significance of Prime Factorization
The prime factorization of a number is unique; this is known as the Fundamental Theorem of Arithmetic. This uniqueness allows for numerous applications:
- Greatest Common Divisor (GCD): Finding the GCD of two numbers involves identifying their prime factors and selecting the common ones raised to the lowest power.
- Least Common Multiple (LCM): The LCM is found by selecting all the prime factors from both numbers, raised to the highest power.
- Cryptology: The security of many encryption methods, like RSA, relies heavily on the difficulty of factoring large numbers into their prime components.
- Modular Arithmetic: Understanding prime factorization is essential for working with modular arithmetic, used extensively in computer science and cryptography.
Applications of Factors and Divisibility in Real-World Scenarios
The seemingly abstract concepts of factors and divisibility find surprising applications in various real-world scenarios:
- Division of Resources: When distributing resources evenly among a group, divisibility plays a vital role in ensuring fair allocation. For example, dividing 10 cookies among 5 children is straightforward (each gets 2), but dividing 10 cookies among 3 children requires a different approach.
- Scheduling and Time Management: Understanding factors helps optimize scheduling. If a task requires 10 hours, and you have 5 days, you can work on it for 2 hours a day.
- Geometry and Measurement: Factors are crucial in calculating areas and volumes. A rectangle with dimensions 2 x 5 has an area of 10 square units.
- Data Structures and Algorithms: In computer science, concepts like factors and divisibility are foundational in algorithms related to sorting, searching, and data organization.
Beyond the Basics: Exploring Further Concepts
The exploration of factors and divisibility extends far beyond the simple example of 10. Several advanced concepts build upon this foundation:
- Perfect Numbers: A perfect number is a positive integer that is equal to the sum of its proper divisors (excluding itself). 6 is the first perfect number (1 + 2 + 3 = 6).
- Amicable Numbers: Two different numbers are amicable if the sum of the proper divisors of each is equal to the other number.
- Highly Composite Numbers: These numbers have more divisors than any smaller positive integer.
- Abundant Numbers: An abundant number is a number for which the sum of its proper divisors is greater than the number itself.
Factors of 10 in Different Number Systems
While our exploration has focused on the decimal (base-10) system, the concept of factors extends to other number systems. The factors of 10 in different bases would change, reflecting the structure and properties of those systems. For instance, in binary (base-2), 10 is represented as 1010, and its factors would be different.
The Importance of Number Theory in Computer Science
Number theory forms a cornerstone of modern computer science. Its applications span diverse areas including:
- Cryptography: As mentioned previously, the security of many encryption algorithms depends heavily on number-theoretic concepts, particularly prime factorization and modular arithmetic.
- Hashing: Hash functions, which map data of arbitrary size to data of a fixed size, often rely on number-theoretic principles for efficiency and collision resistance.
- Data Compression: Some data compression algorithms utilize properties of prime numbers and factorization for efficient data representation.
- Algorithm Analysis: Number theory is essential in analyzing the efficiency and complexity of algorithms.
Conclusion: The Enduring Relevance of Factors
The seemingly simple question of what the factors of 10 are opens a path to a rich landscape of mathematical concepts and practical applications. From basic arithmetic to sophisticated cryptographic techniques, the concepts of factors and divisibility remain fundamental and far-reaching. A deeper understanding of these concepts offers valuable insights across multiple disciplines, underscoring their continued relevance in both theoretical mathematics and practical problem-solving. The seemingly simple number 10, therefore, serves as a gateway to a world of mathematical exploration with profound implications for various fields. Continued exploration in this area remains crucial for advancements in technology and a deeper understanding of the intricate structure of numbers.
Latest Posts
Latest Posts
-
Cbse Class 6th Maths Book Pdf
Apr 04, 2025
-
How Many Atoms Are In Carbon
Apr 04, 2025
-
3 632 Rounded To The Nearest Tenth
Apr 04, 2025
-
2550 50 100 20 100 100 200
Apr 04, 2025
-
What Are Two Kinds Of Fermentation
Apr 04, 2025
Related Post
Thank you for visiting our website which covers about What Are The Factors For 10 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
