What Are The Factor Pairs Of 54
Juapaving
Apr 01, 2025 · 5 min read
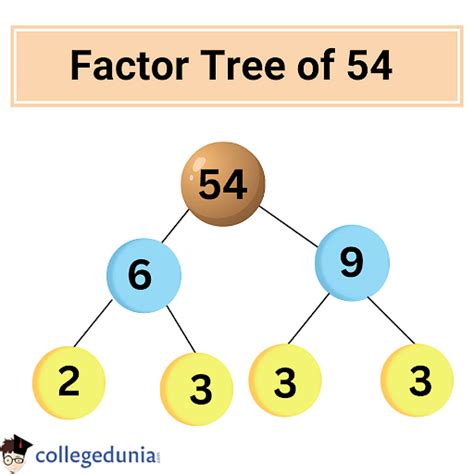
Table of Contents
What are the Factor Pairs of 54? A Deep Dive into Number Theory
Finding the factor pairs of a number is a fundamental concept in number theory, crucial for understanding divisibility, prime factorization, and various mathematical applications. This article delves deep into the process of finding all factor pairs of 54, exploring the underlying principles and demonstrating different methods to achieve this. We'll also discuss the broader implications of factor pairs and their use in more advanced mathematical concepts.
Understanding Factors and Factor Pairs
Before we dive into the specific case of 54, let's establish a clear understanding of the terminology.
-
Factors: Factors of a number are whole numbers that divide the number evenly, leaving no remainder. For example, the factors of 12 are 1, 2, 3, 4, 6, and 12.
-
Factor Pairs: A factor pair consists of two factors whose product equals the original number. For 12, the factor pairs are (1, 12), (2, 6), and (3, 4). Notice that the order within the pair matters; (2, 6) is distinct from (6, 2).
Finding the Factor Pairs of 54: A Systematic Approach
There are several ways to find the factor pairs of 54. Let's explore the most common and efficient methods.
Method 1: The Systematic Listing Method
This method involves systematically listing all the factors of 54 and then pairing them up.
-
Start with 1: 1 is always a factor of any number (except 0). Its pair is 54 (1 x 54 = 54).
-
Check for divisibility by 2: 54 is an even number, so it's divisible by 2. 2 x 27 = 54.
-
Check for divisibility by 3: The sum of digits in 54 (5 + 4 = 9) is divisible by 3, indicating that 54 is divisible by 3. 3 x 18 = 54.
-
Check for divisibility by 6: Since 54 is divisible by both 2 and 3, it's also divisible by 6. 6 x 9 = 54.
-
Check for divisibility by 9: We already know 54 is divisible by 9 because the sum of its digits is 9 (a multiple of 9). 9 x 6 = 54. (Note: this pair has already been identified).
-
Continue until you reach the square root: The square root of 54 is approximately 7.35. We've already found factors larger than this (18, 27, 54), so we can stop our search.
Therefore, the factor pairs of 54 are: (1, 54), (2, 27), (3, 18), (6, 9).
Method 2: Prime Factorization
Prime factorization is a powerful technique for finding all factors of a number. It involves expressing the number as a product of its prime factors. The prime factorization of 54 is 2 x 3 x 3 x 3, or 2 x 3³.
Using the prime factorization, we can systematically generate all possible combinations of factors:
- Using only 2: 2 x 27 = 54
- Using only 3: 3 x 18 = 54; 9 x 6 = 54; 27 x 2 = 54
- Using 2 and 3: Combining prime factors, we get pairs already identified.
This method confirms the factor pairs we found using the systematic listing method.
Visualizing Factor Pairs
Visualizing factor pairs can enhance understanding, especially for larger numbers. We can represent the factor pairs of 54 using a factor tree or a factor rainbow.
Factor Tree for 54
54
/ \
2 27
/ \
3 9
/ \
3 3
This tree shows the prime factorization of 54 (2 x 3 x 3 x 3). Tracing branches back to 54 allows us to deduce the factor pairs.
Factor Rainbow for 54
A factor rainbow visually depicts the factor pairs, connecting pairs that multiply to 54:
1 --- 54 2 --- 27 3 --- 18 6 --- 9
Applications of Factor Pairs
The concept of factor pairs extends beyond simple arithmetic. They are fundamental in:
-
Algebra: Factor pairs are crucial in factoring algebraic expressions and solving quadratic equations.
-
Geometry: They are used in determining the dimensions of rectangles with a given area. For example, a rectangle with an area of 54 square units could have dimensions of 1 x 54, 2 x 27, 3 x 18, or 6 x 9 units.
-
Number Theory: Factor pairs are essential in exploring concepts like greatest common divisors (GCD), least common multiples (LCM), and perfect numbers.
-
Cryptography: Factorization, particularly of very large numbers, plays a critical role in modern cryptography.
Beyond 54: Generalizing the Process
The methods described above can be applied to find the factor pairs of any positive integer. For larger numbers, the systematic listing method might become more tedious, but the prime factorization method remains a powerful and efficient tool. Software and calculators are readily available to aid in finding factor pairs of extremely large numbers, especially those used in cryptography.
Conclusion: Mastering Factor Pairs
Understanding how to find factor pairs is a building block in mathematics. Whether you use the systematic listing method, prime factorization, or a combination of both, the key is to approach the problem systematically and efficiently. The ability to identify factor pairs helps build a deeper understanding of numbers and provides a solid foundation for tackling more advanced mathematical concepts. Mastering this skill enhances problem-solving abilities across various mathematical domains and beyond. Remember to practice consistently and explore the different methods to find the most effective strategy for you. The ability to efficiently find factor pairs will prove invaluable as you progress through your mathematical studies and applications.
Latest Posts
Latest Posts
-
What Tpye Of Reacgion Is Word Bank
Apr 02, 2025
-
How Many Feet Is 103 Inches
Apr 02, 2025
-
What Is The Difference Between A Niche And A Habitat
Apr 02, 2025
-
What Is 30 Percent Of 120
Apr 02, 2025
-
Difference Between Violet And Purple Color
Apr 02, 2025
Related Post
Thank you for visiting our website which covers about What Are The Factor Pairs Of 54 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
