What Are The Factor Pairs Of 50
Juapaving
May 12, 2025 · 5 min read
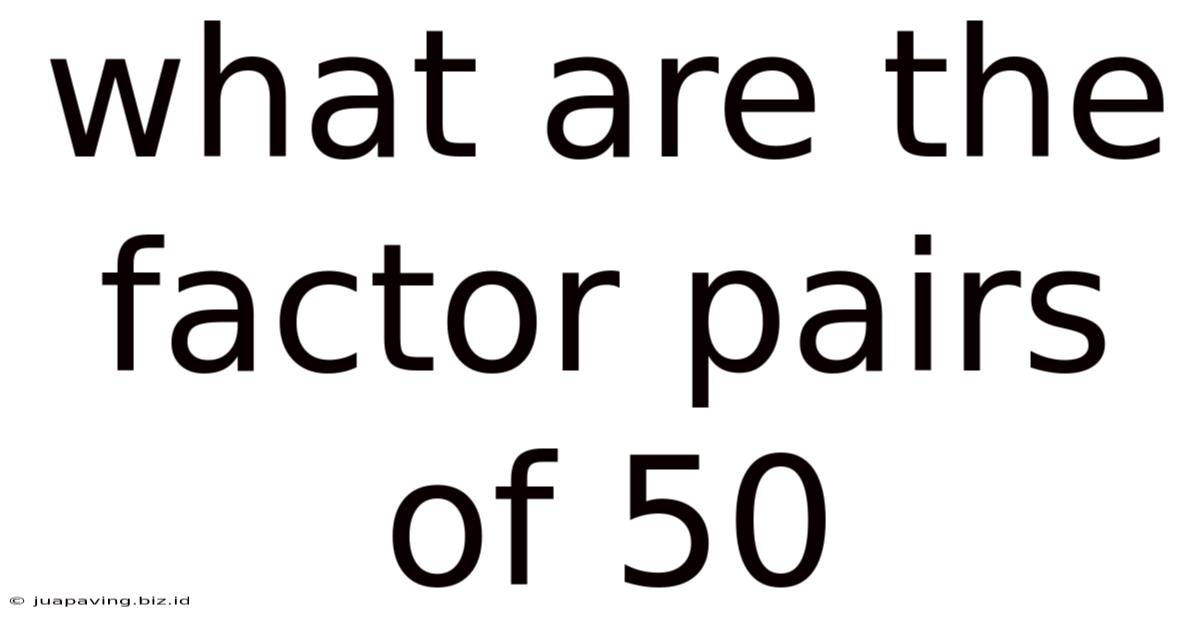
Table of Contents
What are the Factor Pairs of 50? A Deep Dive into Number Theory
Finding the factor pairs of a number might seem like a simple task, especially for a relatively small number like 50. However, understanding the concept of factor pairs and how to find them is fundamental to grasping key concepts in number theory and algebra. This article will not only explore the factor pairs of 50 but also delve into the broader significance of factorization and its applications. We'll examine different methods for finding factor pairs and discuss why this seemingly basic concept holds significant weight in more advanced mathematical contexts.
Understanding Factors and Factor Pairs
Before we jump into finding the factor pairs of 50, let's clarify the definitions.
Factors: Factors of a number are whole numbers that divide the number evenly (without leaving a remainder). For instance, the factors of 12 are 1, 2, 3, 4, 6, and 12 because each of these numbers divides 12 without a remainder.
Factor Pairs: A factor pair consists of two factors that, when multiplied together, result in the original number. For example, the factor pairs of 12 are (1, 12), (2, 6), and (3, 4). Notice that the order matters; (2, 6) is considered a different factor pair than (6, 2), although they contain the same factors.
Finding the Factor Pairs of 50
Now, let's find all the factor pairs of 50. We can systematically approach this using a few methods:
Method 1: Listing Factors
This method involves listing all the factors of 50 and then pairing them to find the products that equal 50.
- Start with 1: 1 is always a factor of any whole number. Its pair is 50 (1 x 50 = 50).
- Check for 2: 50 is an even number, so 2 is a factor. Its pair is 25 (2 x 25 = 50).
- Check for 3: 50 is not divisible by 3 (5+0=5, which is not divisible by 3).
- Check for 4: 50 is not divisible by 4.
- Check for 5: 50 is divisible by 5. Its pair is 10 (5 x 10 = 50).
- Check for numbers greater than 5: We've already found all the factors because any factor larger than 7 would necessitate a paired factor smaller than 7, which we've already checked.
Therefore, the factor pairs of 50 are (1, 50), (2, 25), and (5, 10).
Method 2: Prime Factorization
Prime factorization is a powerful technique that breaks a number down into its prime factors (numbers divisible only by 1 and themselves). This method is particularly useful for larger numbers.
-
Find the prime factorization of 50: 50 can be expressed as 2 x 5 x 5, or 2 x 5².
-
Use the prime factors to build factor pairs: From the prime factorization, we can systematically build factor pairs:
- 1 x (2 x 5 x 5) = 50 => (1, 50)
- 2 x (5 x 5) = 50 => (2, 25)
- 5 x (2 x 5) = 50 => (5, 10)
- (2 x 5) x 5 = 50 => (10,5) - already covered
- (5 x 5) x 2 = 50 => (25,2) - already covered
- (2 x 5 x 5) x 1 = 50 => (50,1) - already covered
This method ensures we don't miss any factor pairs. We still arrive at the same three unique factor pairs: (1, 50), (2, 25), and (5, 10).
The Significance of Factor Pairs
The seemingly simple exercise of finding factor pairs has far-reaching implications in mathematics and its applications:
1. Greatest Common Factor (GCF) and Least Common Multiple (LCM):** Factor pairs are crucial for determining the GCF and LCM of two or more numbers. The GCF is the largest factor common to all numbers, while the LCM is the smallest multiple common to all numbers. Finding the prime factorization of each number allows for efficient calculation of the GCF and LCM, which are essential concepts in simplifying fractions, solving equations, and working with ratios and proportions.
2. Algebraic Factoring:** Factoring is a fundamental skill in algebra. It involves expressing an algebraic expression as a product of simpler expressions. Understanding factor pairs helps to break down polynomials and solve quadratic equations, which are essential components in various fields, including engineering, physics, and finance.
3. Cryptography:** Factorization plays a vital role in cryptography. Modern encryption techniques rely on the difficulty of factoring very large numbers into their prime factors. This mathematical principle underpins many secure online transactions and data protection methods.
4. Number Theory:** Factor pairs are a key concept in number theory, a branch of mathematics focused on the properties of integers. Investigating the factors of numbers leads to explorations of prime numbers, perfect numbers, and other intriguing number patterns.
5. Real-World Applications:** The concepts of factors and multiples appear in numerous everyday contexts. Imagine dividing a group of 50 people into smaller teams of equal size. Finding the factor pairs of 50 helps determine the possible team sizes (1, 2, 5, 10, 25, 50). This principle extends to various real-world scenarios involving division, distribution, and arrangement.
Exploring Beyond 50: Expanding the Concept
While we've focused on the factor pairs of 50, the methods discussed—listing factors and prime factorization—are applicable to any whole number. Let's briefly consider some other numbers to illustrate:
-
Factor Pairs of 100: (1, 100), (2, 50), (4, 25), (5, 20), (10, 10). Notice the perfect square aspect; 100 is 10 squared, resulting in a single factor pair where both factors are equal.
-
Factor Pairs of 121: (1, 121), (11, 11). 121 is 11 squared, similar to 100.
-
Factor Pairs of a Prime Number (e.g., 7): (1, 7). Prime numbers only have two factors: 1 and themselves.
Conclusion: The Enduring Importance of Factor Pairs
Finding the factor pairs of 50, while seemingly a simple task, provides a gateway to understanding essential concepts in mathematics and its applications across various disciplines. From the practical application of dividing groups to the more complex principles of cryptography and algebra, the ability to find factor pairs and understand the underlying principles of factorization is an invaluable skill. This seemingly simple mathematical concept holds the key to unlocking more complex and significant mathematical explorations. The techniques described here can be applied to any number, leading to a deeper understanding of numbers and their properties. Remember to practice these techniques to enhance your understanding and mastery of factorization.
Latest Posts
Latest Posts
-
In Which Phase Does Crossing Over Occur
May 13, 2025
-
Lowest Common Multiple Of 24 And 42
May 13, 2025
-
Which Shape Has Exactly 4 Lines Of Symmetry
May 13, 2025
-
When Acid Reacts With Base What Compounds Are Formed
May 13, 2025
-
Difference Between An Act And Law
May 13, 2025
Related Post
Thank you for visiting our website which covers about What Are The Factor Pairs Of 50 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.