What Are The Common Factors Of 18 And 24
Juapaving
Mar 26, 2025 · 5 min read
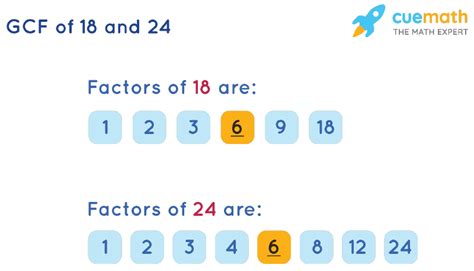
Table of Contents
Unraveling the Common Factors of 18 and 24: A Deep Dive into Number Theory
Finding the common factors of two numbers might seem like a simple arithmetic exercise, but it's a fundamental concept in number theory with far-reaching applications in mathematics and computer science. This article will explore the common factors of 18 and 24 in detail, delving into the methods used to identify them, explaining the underlying mathematical principles, and showcasing how this concept connects to more advanced mathematical ideas. We'll also touch upon practical applications of finding common factors.
Understanding Factors and Common Factors
Before diving into the specifics of 18 and 24, let's establish a clear understanding of the terminology.
-
Factors: A factor of a number is any number that divides it evenly without leaving a remainder. For instance, the factors of 12 are 1, 2, 3, 4, 6, and 12.
-
Common Factors: Common factors are numbers that are factors of two or more numbers. They are the numbers that divide both numbers evenly.
Our goal is to find all the common factors of 18 and 24.
Method 1: Listing Factors
The most straightforward method is to list all the factors of each number and then identify the common ones.
Factors of 18: 1, 2, 3, 6, 9, 18
Factors of 24: 1, 2, 3, 4, 6, 8, 12, 24
By comparing the two lists, we can easily see the common factors: 1, 2, 3, and 6.
This method works well for smaller numbers, but it becomes cumbersome and inefficient as the numbers get larger.
Method 2: Prime Factorization
A more efficient and systematic approach involves prime factorization. Prime factorization is the process of expressing a number as a product of its prime factors (numbers divisible only by 1 and themselves).
Prime Factorization of 18:
18 = 2 x 9 = 2 x 3 x 3 = 2 x 3²
Prime Factorization of 24:
24 = 2 x 12 = 2 x 2 x 6 = 2 x 2 x 2 x 3 = 2³ x 3
Now, to find the common factors, we look for the prime factors that appear in both factorizations. Both 18 and 24 contain the prime factors 2 and 3.
- Common Prime Factors: 2 and 3
To find all the common factors, we consider all possible combinations of these common prime factors:
- 2¹ = 2
- 3¹ = 3
- 2¹ x 3¹ = 6
- 2⁰ x 3⁰ = 1 (Remember, any number raised to the power of 0 is 1)
Therefore, the common factors of 18 and 24 are 1, 2, 3, and 6. This method is more efficient for larger numbers as it provides a structured way to find the common factors.
Method 3: Greatest Common Divisor (GCD)
The greatest common divisor (GCD), also known as the highest common factor (HCF), is the largest number that divides both numbers without leaving a remainder. Once we find the GCD, we can easily determine all other common factors.
There are several ways to calculate the GCD:
- Euclidean Algorithm: This is an efficient algorithm for finding the GCD of two numbers. It involves repeatedly applying the division algorithm until the remainder is 0. The last non-zero remainder is the GCD.
Let's apply the Euclidean algorithm to 18 and 24:
- Divide 24 by 18: 24 = 18 x 1 + 6
- Divide 18 by the remainder 6: 18 = 6 x 3 + 0
The last non-zero remainder is 6, so the GCD of 18 and 24 is 6.
- Prime Factorization Method: We can also use prime factorization to find the GCD. We take the lowest power of each common prime factor and multiply them together.
From the prime factorizations above:
18 = 2¹ x 3² 24 = 2³ x 3¹
The common prime factors are 2 and 3. The lowest power of 2 is 2¹, and the lowest power of 3 is 3¹. Therefore, the GCD is 2¹ x 3¹ = 6.
Once we have the GCD (6), we know that all the common factors must be divisors of the GCD. The divisors of 6 are 1, 2, 3, and 6, confirming our previous results.
Applications of Finding Common Factors
Finding common factors is not merely an abstract mathematical exercise; it has practical applications in various fields:
-
Simplification of Fractions: Finding the GCD is crucial for simplifying fractions to their lowest terms. For example, the fraction 18/24 can be simplified by dividing both the numerator and denominator by their GCD (6), resulting in the simplified fraction 3/4.
-
Modular Arithmetic: Common factors play a significant role in modular arithmetic, which is used in cryptography and computer science.
-
Geometry: Finding common factors is useful in solving geometric problems involving area and volume calculations. For example, determining the largest square tile that can perfectly cover a rectangular floor requires finding the GCD of the floor's dimensions.
-
Scheduling and Planning: In project management and scheduling, determining the common factors between different task durations helps in optimizing timelines and resource allocation.
-
Music Theory: The concept of common factors is used in music theory to understand harmonic relationships between different musical intervals.
Expanding the Concept: Least Common Multiple (LCM)
While we've focused on common factors, it's important to mention the closely related concept of the least common multiple (LCM). The LCM is the smallest number that is a multiple of both numbers. The GCD and LCM are related by the following formula:
LCM(a, b) x GCD(a, b) = a x b
For 18 and 24:
LCM(18, 24) x GCD(18, 24) = 18 x 24
LCM(18, 24) x 6 = 432
LCM(18, 24) = 72
The LCM of 18 and 24 is 72. This means 72 is the smallest number that is divisible by both 18 and 24.
Conclusion
Finding the common factors of 18 and 24, while seemingly simple, provides a gateway to understanding fundamental concepts in number theory, such as prime factorization, the greatest common divisor, and the least common multiple. These concepts are not just abstract mathematical ideas but have tangible applications across various disciplines, highlighting the practical significance of even the most basic mathematical principles. By mastering these concepts, we gain a deeper appreciation for the structure and beauty of mathematics and its pervasive influence on the world around us. The methods discussed—listing factors, prime factorization, and the Euclidean algorithm—provide a robust toolkit for tackling similar problems with larger and more complex numbers. Understanding these methods empowers us to approach more advanced mathematical concepts with confidence and skill.
Latest Posts
Latest Posts
-
Diagram Of Animal And Plant Cell
Mar 29, 2025
-
Primary Spermatocyte Is Haploid Or Diploid
Mar 29, 2025
-
Round 32 To The Nearest Ten
Mar 29, 2025
-
Shape With 12 Edges And 6 Faces
Mar 29, 2025
-
How Many Factors Does 10 Have
Mar 29, 2025
Related Post
Thank you for visiting our website which covers about What Are The Common Factors Of 18 And 24 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
