What Are All The Factors Of 90
Juapaving
Apr 07, 2025 · 5 min read
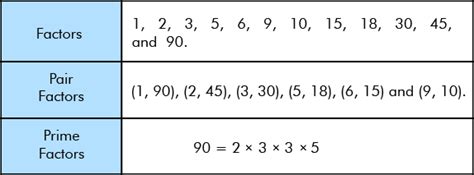
Table of Contents
What Are All the Factors of 90? A Deep Dive into Factorization
Finding all the factors of a number might seem like a simple mathematical task, but understanding the process reveals fascinating insights into number theory and its applications. This article delves into the complete factorization of 90, exploring various methods, underlying concepts, and practical applications. We'll move beyond simply listing the factors to understanding why these numbers are factors and how this knowledge can be useful in more complex mathematical scenarios.
Understanding Factors and Factorization
Before we dive into the specifics of 90, let's establish a clear definition. A factor (or divisor) of a number is a whole number that divides the original number exactly without leaving a remainder. Factorization is the process of breaking down a number into its factors. For example, the factors of 12 are 1, 2, 3, 4, 6, and 12 because each of these numbers divides 12 evenly.
Prime Factorization: The Foundation
A crucial concept in factorization is the prime factorization. A prime number is a whole number greater than 1 that has only two divisors: 1 and itself (e.g., 2, 3, 5, 7, 11...). The prime factorization of a number is its representation as a product of prime numbers. This representation is unique for every number (Fundamental Theorem of Arithmetic).
Finding the prime factorization is a cornerstone of finding all factors. Once we have the prime factorization, we can systematically derive all other factors.
Finding the Factors of 90: A Step-by-Step Approach
Let's now apply these concepts to find all the factors of 90.
1. Prime Factorization of 90
We begin by finding the prime factorization of 90. We can use a factor tree:
- 90 is divisible by 2: 90 = 2 x 45
- 45 is divisible by 3: 45 = 3 x 15
- 15 is divisible by 3: 15 = 3 x 5
- 5 is a prime number.
Therefore, the prime factorization of 90 is 2 x 3 x 3 x 5, or 2 x 3² x 5.
2. Deriving All Factors from the Prime Factorization
Now that we have the prime factorization (2 x 3² x 5), we can systematically generate all the factors. We do this by considering all possible combinations of the prime factors:
- Using only one prime factor: 2, 3, 5
- Using two prime factors: 2 x 3 = 6, 2 x 5 = 10, 3 x 3 = 9, 3 x 5 = 15
- Using three prime factors: 2 x 3 x 3 = 18, 2 x 3 x 5 = 30, 3 x 3 x 5 = 45
- Using all four prime factors: 2 x 3 x 3 x 5 = 90
- And don't forget 1! 1 is always a factor of any number.
Therefore, all the factors of 90 are: 1, 2, 3, 5, 6, 9, 10, 15, 18, 30, 45, and 90.
Beyond the List: Understanding the Significance of Factors
The factors of 90 aren't just a random collection of numbers. They hold mathematical significance in several contexts:
1. Divisibility Rules
Understanding factors helps us determine divisibility rules. For instance, since 90 is divisible by 2, it's an even number. Since it's divisible by 3, the sum of its digits (9) is divisible by 3. Since it's divisible by 5, it ends in 0 or 5.
2. Greatest Common Divisor (GCD) and Least Common Multiple (LCM)
Factors play a vital role in finding the GCD and LCM of two or more numbers. The GCD is the largest number that divides all the given numbers without leaving a remainder. The LCM is the smallest number that is a multiple of all the given numbers.
For example, let's find the GCD and LCM of 90 and 120:
- Prime factorization of 120: 2³ x 3 x 5
- GCD(90, 120): The common prime factors are 2, 3, and 5. The lowest power of each common factor is 2¹, 3¹, and 5¹. Therefore, GCD(90, 120) = 2 x 3 x 5 = 30.
- LCM(90, 120): We consider all prime factors from both factorizations, taking the highest power of each: 2³, 3¹, 5¹. Therefore, LCM(90, 120) = 2³ x 3 x 5 = 360.
3. Applications in Algebra and Geometry
Factors are fundamental in algebraic manipulations, such as factoring polynomials. They also appear in geometric problems, such as finding dimensions of rectangles with a given area. For instance, if the area of a rectangle is 90 square units, the possible dimensions are pairs of factors of 90 (e.g., 9 x 10, 6 x 15, 2 x 45, etc.).
4. Number Theory and Cryptography
The study of factors, particularly prime factorization, is central to number theory. This field has significant applications in cryptography, where the difficulty of factoring large numbers into their prime factors forms the basis of many encryption algorithms.
Advanced Factorization Techniques
While the factor tree method is effective for smaller numbers like 90, larger numbers require more sophisticated techniques:
1. Trial Division
This method involves systematically dividing the number by all prime numbers up to its square root. If a prime number divides the number evenly, it's a factor.
2. Pollard's Rho Algorithm
This is a probabilistic algorithm used for factoring large composite numbers. It's particularly effective for finding small factors.
3. Quadratic Sieve and General Number Field Sieve
These are advanced algorithms used for factoring extremely large numbers, often employed in cryptography research.
Conclusion: The Ubiquity of Factors
This in-depth exploration of the factors of 90 showcases the foundational role of factorization in mathematics. While finding the factors of a small number like 90 might seem straightforward, the underlying principles and their applications extend far beyond simple calculations. From divisibility rules to complex cryptographic algorithms, understanding factors is crucial for navigating various mathematical and computational domains. The seemingly simple act of finding all the factors of 90 opens a door to a rich and fascinating world of number theory and its diverse applications.
Latest Posts
Latest Posts
-
How Many Electrons Does Oxygen Have In Its Outermost Shell
Apr 07, 2025
-
What Is Not Necessary For Photosynthesis
Apr 07, 2025
-
Magnesium Oxide And Hcl Balanced Equation
Apr 07, 2025
-
How Many Seconds In 365 Days
Apr 07, 2025
-
How Many Centimeters Are In 5 Meters
Apr 07, 2025
Related Post
Thank you for visiting our website which covers about What Are All The Factors Of 90 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.