Two Lines Cut By A Transversal
Juapaving
Apr 06, 2025 · 6 min read
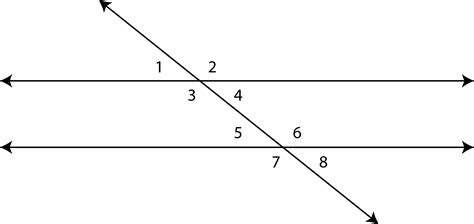
Table of Contents
Two Lines Cut by a Transversal: A Comprehensive Exploration
When two lines are intersected by a third line, called a transversal, a fascinating array of geometric relationships emerges. This seemingly simple scenario forms the basis for understanding many fundamental concepts in geometry, and it has significant implications in various fields, from architecture and engineering to computer graphics and cartography. This article delves into the intricacies of two lines cut by a transversal, exploring the theorems, postulates, and practical applications associated with this geometric configuration.
Understanding the Basics: Lines and Transversals
Before we dive into the specifics of the relationships formed, let's define our key terms:
-
Lines: In geometry, a line is a straight, one-dimensional figure extending infinitely in both directions. We often represent lines using lowercase letters (e.g., line l, line m) or by naming two points on the line (e.g., line AB).
-
Transversal: A transversal is a line that intersects two or more other lines at distinct points. It's crucial to understand that the transversal must intersect the other lines at separate points; otherwise, it wouldn't create the relationships we're interested in studying.
When a transversal intersects two lines, eight angles are formed. These angles are categorized into several types based on their relative positions:
Types of Angles Formed:
-
Interior Angles: These angles lie between the two lines intersected by the transversal. There are four interior angles in total.
-
Exterior Angles: These angles lie outside the two lines intersected by the transversal. There are also four exterior angles in total.
-
Consecutive Interior Angles: These are pairs of interior angles that are on the same side of the transversal. They are also sometimes called same-side interior angles.
-
Alternate Interior Angles: These are pairs of interior angles that are on opposite sides of the transversal and between the two lines.
-
Corresponding Angles: These are pairs of angles, one interior and one exterior, that are on the same side of the transversal and in corresponding positions relative to the two lines.
-
Alternate Exterior Angles: These are pairs of exterior angles that are on opposite sides of the transversal and outside the two lines.
The Power of Parallel Lines: Theorems and Postulates
The most significant relationships between angles formed when a transversal intersects two lines arise when the lines are parallel. This scenario leads to several crucial theorems:
1. Corresponding Angles Theorem:
If two parallel lines are cut by a transversal, then the corresponding angles are congruent (equal in measure). This theorem provides a powerful tool for determining the measures of angles when dealing with parallel lines. For example, if one corresponding angle is measured as 60°, then its corresponding angle on the other line will also measure 60°.
2. Alternate Interior Angles Theorem:
If two parallel lines are cut by a transversal, then the alternate interior angles are congruent. This theorem offers another way to establish equality between angles when parallelism is involved. Knowing the measure of one alternate interior angle allows you to directly determine the measure of its counterpart.
3. Alternate Exterior Angles Theorem:
Similar to the alternate interior angles theorem, if two parallel lines are cut by a transversal, the alternate exterior angles are congruent. This theorem extends the congruence relationship to the exterior angles, providing additional tools for angle calculations.
4. Consecutive Interior Angles Theorem:
If two parallel lines are cut by a transversal, then consecutive interior angles are supplementary (their measures add up to 180°). This theorem highlights the relationship between angles on the same side of the transversal. It's essential for solving problems where the sum of angles is known.
When Lines are Not Parallel: Exploring Non-Parallel Scenarios
The relationships described above are specific to parallel lines. When the two lines intersected by the transversal are not parallel, the angle relationships change significantly. In this case, none of the theorems mentioned previously hold true. Instead, we rely on the general principles of angle addition and supplementary angles to solve problems.
For example, consecutive interior angles would no longer be supplementary, and alternate interior angles would not be congruent. The specific relationships will depend on the angles formed between the lines. Calculating the angles will require more information about the angles themselves or the relationship between the lines.
Practical Applications: Geometry in the Real World
The concepts discussed here have far-reaching practical applications:
-
Architecture and Construction: Understanding the relationships between angles formed by transversals is crucial in designing stable and structurally sound buildings. Parallel lines and their intersection with transversals are fundamental in ensuring accurate measurements and construction.
-
Civil Engineering: Road design, bridge construction, and surveying all rely heavily on geometric principles. The accurate measurement and calculation of angles are paramount to ensuring the safety and functionality of these structures.
-
Computer Graphics: In computer-aided design (CAD) and computer graphics, the manipulation of lines and angles is fundamental. Understanding transversals and their relationships is crucial for creating accurate and realistic representations of objects and environments.
-
Cartography: Mapmaking utilizes geometric principles to accurately represent the Earth's surface. Understanding angles and parallel lines is crucial for creating accurate maps and projections.
-
Photography: Understanding perspective and how lines converge can improve composition and create visually appealing images. Knowledge of parallel lines and transversals helps photographers anticipate and control the distortion of lines in their photos.
Solving Problems: A Step-by-Step Approach
Let's illustrate the application of these theorems with an example.
Problem: Two parallel lines, line l and line m, are intersected by a transversal, line t. One of the alternate interior angles measures 75°. Find the measures of all other angles formed by the intersection.
Solution:
-
Identify Parallel Lines and Transversal: We are given that lines l and m are parallel, and line t is the transversal.
-
Identify the Given Angle: One alternate interior angle measures 75°.
-
Apply Theorems:
-
Alternate Interior Angles Theorem: Since the lines are parallel, the other alternate interior angle also measures 75°.
-
Corresponding Angles Theorem: The corresponding angles to the 75° angles also measure 75°.
-
Consecutive Interior Angles Theorem: Consecutive interior angles are supplementary, so their measures add up to 180°. Therefore, the consecutive interior angles measure 180° - 75° = 105°.
-
-
Verify: All angles should add up to a total of 360°. Check if the calculated angles meet this condition.
Advanced Concepts and Extensions
The study of two lines cut by a transversal forms the foundation for more advanced geometric concepts, including:
-
Proving Lines Parallel: Conversely, if any of the angle relationships discussed (corresponding, alternate interior, alternate exterior, or consecutive interior) are found to be true, it can be concluded that the two lines are parallel. This is crucial in geometric proofs and constructions.
-
Triangles and Polygons: The angles formed by a transversal intersecting two parallel lines often become integral parts of triangles and other polygons, leading to further investigations of their properties.
-
Three or More Parallel Lines: The principles can be extended to scenarios where a transversal intersects three or more parallel lines, creating even more complex relationships among the angles.
Conclusion
The seemingly simple scenario of two lines intersected by a transversal unveils a rich tapestry of geometric relationships. Understanding these relationships is fundamental to solving various geometric problems and has widespread applications across many fields. From architecture and engineering to computer graphics and cartography, the principles discussed here are essential tools for tackling real-world challenges. Mastering the concepts of corresponding, alternate interior, alternate exterior, and consecutive interior angles, along with their implications for parallel lines, is crucial for anyone seeking a deeper understanding of geometry and its practical applications. This thorough exploration provides a strong foundation for further study in advanced geometric concepts.
Latest Posts
Latest Posts
-
How Many Factors Does 81 Have
Apr 08, 2025
-
Interval Of Convergence Power Series Calculator
Apr 08, 2025
-
Which Organelle Captures Energy From Sunlight
Apr 08, 2025
-
Write The Complete Ground State Electron Configuration Of Arsenic
Apr 08, 2025
-
How To Find The Amount Of Moles In A Compound
Apr 08, 2025
Related Post
Thank you for visiting our website which covers about Two Lines Cut By A Transversal . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.