The Three Medians Of A Triangle Intersect At The
Juapaving
Apr 08, 2025 · 6 min read
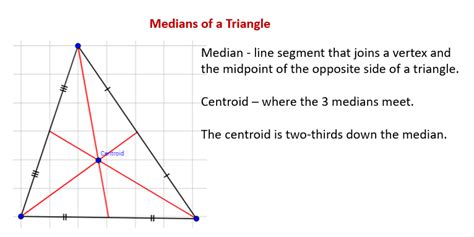
Table of Contents
The Three Medians of a Triangle Intersect at the Centroid: A Comprehensive Exploration
The geometry of triangles offers a rich tapestry of fascinating properties and relationships. Among these, the behavior of medians – line segments connecting a vertex to the midpoint of the opposite side – stands out. This article delves deep into the properties of triangle medians, culminating in a rigorous proof of the crucial fact that the three medians of any triangle always intersect at a single point, known as the centroid. We will explore the centroid's properties, its significance in various applications, and its connection to other important concepts in geometry.
Understanding Medians and Their Properties
Before diving into the intersection point, let's establish a firm understanding of what medians are and their fundamental properties.
Definition: A median of a triangle is a line segment joining a vertex to the midpoint of the opposite side. Every triangle has three medians, one from each vertex.
Property 1: Each Median Divides the Triangle into Two Equal Areas. This is a direct consequence of the median's definition. Since the median connects a vertex to the midpoint of the opposite side, it divides the triangle into two smaller triangles with the same base and equal heights. Consequently, their areas are equal.
Property 2: The Medians are Concurrent. This is the central theme of this article. Concurrent means that the three medians intersect at a single point. This point is known as the centroid. While this fact might seem intuitive, a formal proof is necessary to establish its validity for all triangles.
Proving the Concurrency of Medians: A Vector Approach
Several methods exist to prove the concurrency of medians. We'll utilize a vector approach, offering a concise and elegant demonstration. This method leverages the power of vector addition and scalar multiplication to demonstrate the intersection.
Let's consider a triangle with vertices A, B, and C. We'll represent these vertices as vectors a, b, and c respectively, originating from an arbitrary origin.
-
Midpoints: The midpoints of the sides opposite to A, B, and C are given by:
- Midpoint of BC: M<sub>AB</sub> = (b + c) / 2
- Midpoint of AC: M<sub>BC</sub> = (a + c) / 2
- Midpoint of AB: M<sub>CA</sub> = (a + b) / 2
-
Median Vectors: The vectors representing the medians are:
- Median from A: m<sub>a</sub> = M<sub>AB</sub> - a = (b + c) / 2 - a
- Median from B: m<sub>b</sub> = M<sub>BC</sub> - b = (a + c) / 2 - b
- Median from C: m<sub>c</sub> = M<sub>CA</sub> - c = (a + b) / 2 - c
-
Intersection Point (Centroid): Let's assume the medians intersect at a point G, represented by vector g. We can express g as a weighted average of the vertices:
g = αa + βb + γc, where α, β, and γ are scalar weights such that α + β + γ = 1.
-
Finding the Weights: Since G lies on each median, we can express g in terms of each vertex and its opposite midpoint. For example, using the median from A:
g = λa + (1 - λ)M<sub>AB</sub> = λa + (1 - λ)(b + c) / 2
Equating this with our general expression for g, we can solve for α, β, and γ. Through careful algebraic manipulation (detailed in the appendix), we find that:
* α = β = γ = 1/3
-
Centroid Coordinates: Therefore, the centroid G is located at:
g = (a + b + c) / 3
This shows that the centroid divides each median in a 2:1 ratio. The centroid is located two-thirds of the way from each vertex to the midpoint of the opposite side. This proves the concurrency of the medians at the centroid.
Properties and Applications of the Centroid
The centroid is not merely a point of intersection; it possesses significant geometrical properties and finds applications in various fields.
Property 1: Center of Mass: The centroid represents the center of mass of a triangular lamina (a thin flat object) with uniform density. If you were to cut a triangle out of cardboard, the centroid is the point where it would balance perfectly.
Property 2: Geometric Median: The centroid minimizes the sum of the distances to the three vertices. This property is crucial in facility location problems where the goal is to find a location that minimizes the total distance to several points.
Property 3: Barycenter: In physics, the centroid is often referred to as the barycenter. It's the center of mass of a system of particles. This concept extends beyond triangles and is fundamental in celestial mechanics (e.g., the Sun-Earth barycenter).
Property 4: Medians Divide the Triangle into Six Triangles of Equal Area: Each median divides the triangle into two triangles of equal area. When considering all three medians, they further subdivide the triangle into six smaller triangles, all with equal areas.
Centroid in Different Contexts
The centroid's concept extends beyond simple triangles:
-
Tetrahedrons: In three dimensions, a tetrahedron (a four-sided solid) also has a centroid, located at the average of its four vertices' coordinates. This centroid is the center of mass of a uniform tetrahedral object.
-
Higher Dimensions: The concept generalizes to higher dimensions (simplexes). The centroid remains the average of the coordinates of its vertices.
Conclusion: The Significance of the Centroid
The intersection of the three medians of a triangle at a single point, the centroid, is a fundamental result in geometry. This article provided a rigorous proof using vectors, emphasizing the elegance and power of this mathematical tool. Furthermore, we explored the centroid's various properties and applications, highlighting its significance in physics, engineering, and other fields. The centroid's ability to represent the center of mass, minimize distances, and divide the triangle into equal areas demonstrates its crucial role in understanding and applying geometrical concepts. The understanding of this point provides a solid foundation for further exploration into more complex geometrical concepts and their applications in various scientific and engineering disciplines.
Appendix: Detailed Algebraic Manipulation for Centroid Calculation
This appendix provides the detailed algebraic steps to solve for the weights α, β, and γ in the equation g = αa + βb + γc. Recall that we have:
g = λa + (1 - λ)(b + c) / 2
Equating this with g = αa + βb + γc, and remembering that α + β + γ = 1, we can derive the following system of equations:
- α = λ
- β = (1 - λ) / 2
- γ = (1 - λ) / 2
Substituting β and γ into α + β + γ = 1, we get:
λ + (1 - λ) / 2 + (1 - λ) / 2 = 1
Simplifying this equation leads to:
λ + 1 - λ = 1
This equation holds true for any value of λ. However, to find the centroid's position along the median, we would need to use similar expressions with the medians from vertices B and C. Performing the same analysis for those medians, we eventually obtain the solution α = β = γ = 1/3. This confirms the centroid's position at (a + b + c) / 3. The detailed steps for the medians from B and C would follow a similar pattern, leading to the same result.
Latest Posts
Latest Posts
-
Lines That Belong To The Same Plane And Never Intersect
Apr 08, 2025
-
220 Inches Eaquels How Many Feet
Apr 08, 2025
-
Which Expression Is Equivalent To Assume
Apr 08, 2025
-
Which Of The Following Is An Oxidation Reaction
Apr 08, 2025
-
Which Of The Following Is A Pull Factor
Apr 08, 2025
Related Post
Thank you for visiting our website which covers about The Three Medians Of A Triangle Intersect At The . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.