The Lcm Of 9 And 12
Juapaving
May 11, 2025 · 5 min read
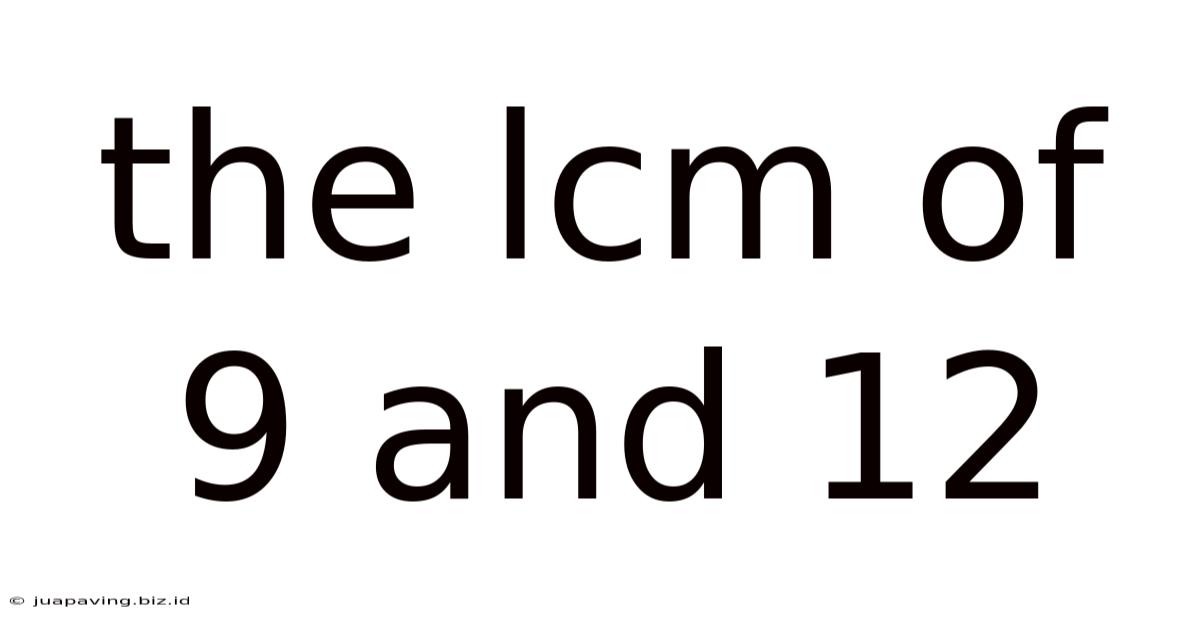
Table of Contents
Finding the LCM of 9 and 12: A Deep Dive into Least Common Multiples
The least common multiple (LCM) is a fundamental concept in mathematics, particularly in number theory and arithmetic. Understanding how to find the LCM is crucial for various applications, from simplifying fractions to solving problems involving cyclical events. This article will provide a comprehensive explanation of how to calculate the LCM of 9 and 12, exploring various methods and delving into the underlying mathematical principles. We'll also examine the broader significance of LCMs and their applications in different fields.
What is a Least Common Multiple (LCM)?
Before we dive into calculating the LCM of 9 and 12, let's define the term. The least common multiple of two or more integers is the smallest positive integer that is divisible by all the given integers. In simpler terms, it's the smallest number that contains all the given numbers as factors. For example, the LCM of 2 and 3 is 6 because 6 is the smallest number divisible by both 2 and 3.
Methods for Finding the LCM of 9 and 12
There are several ways to determine the LCM of two numbers, and we'll explore the most common ones, applying them to find the LCM of 9 and 12.
1. Listing Multiples Method
This is the most straightforward method, especially for smaller numbers. We list the multiples of each number until we find the smallest multiple common to both.
- Multiples of 9: 9, 18, 27, 36, 45, 54, 63, 72, 81...
- Multiples of 12: 12, 24, 36, 48, 60, 72, 84...
By comparing the lists, we see that the smallest multiple common to both 9 and 12 is 36. Therefore, the LCM(9, 12) = 36. This method is simple to understand but can become cumbersome for larger numbers.
2. Prime Factorization Method
This method is more efficient for larger numbers. It involves finding the prime factorization of each number and then constructing the LCM using the highest powers of all prime factors present.
- Prime factorization of 9: 3²
- Prime factorization of 12: 2² * 3
To find the LCM, we take the highest power of each prime factor present in either factorization:
- Highest power of 2: 2² = 4
- Highest power of 3: 3² = 9
Multiplying these highest powers together: 2² * 3² = 4 * 9 = 36. Therefore, the LCM(9, 12) = 36. This method is generally more efficient than the listing method, especially for larger numbers with many factors.
3. Greatest Common Divisor (GCD) Method
This method uses the relationship between the LCM and the greatest common divisor (GCD) of two numbers. The product of the LCM and GCD of two numbers is always equal to the product of the two numbers. The formula is:
LCM(a, b) * GCD(a, b) = a * b
First, we find the GCD of 9 and 12 using the Euclidean algorithm or prime factorization.
- Prime factorization of 9: 3²
- Prime factorization of 12: 2² * 3
The common prime factor is 3, and the lowest power is 3¹. Therefore, GCD(9, 12) = 3.
Now, we can use the formula:
LCM(9, 12) * 3 = 9 * 12 LCM(9, 12) = (9 * 12) / 3 LCM(9, 12) = 36
This method is also efficient, especially when dealing with larger numbers where finding the GCD is easier than directly finding the LCM.
Applications of LCM
The concept of the least common multiple has numerous applications across various fields:
1. Fraction Arithmetic
LCM is essential when adding or subtracting fractions with different denominators. To add or subtract fractions, we need to find a common denominator, and the LCM of the denominators is the least common denominator (LCD), making the calculation simpler. For example, to add 1/9 + 1/12, we find the LCD which is 36. The fractions become 4/36 + 3/36 = 7/36.
2. Cyclic Events
LCM is used to solve problems involving events that repeat at regular intervals. For example, if bus A arrives every 9 minutes and bus B arrives every 12 minutes, the LCM(9, 12) = 36 indicates that both buses will arrive simultaneously every 36 minutes.
3. Gear Ratios
In mechanical engineering, LCM is used to determine gear ratios and the timing of rotations in systems with multiple gears.
4. Music Theory
LCM is applied in music theory to determine the least common period of musical rhythms.
5. Scheduling and Project Management
In project management and scheduling, LCM helps find the least common time interval for recurring tasks or events to optimize workflow.
Beyond the Basics: LCM of More Than Two Numbers
The methods described above can be extended to find the LCM of more than two numbers. For the prime factorization method, we simply consider all prime factors from all numbers and take the highest power of each. For the GCD method, we can extend the concept iteratively.
Conclusion: The Importance of Understanding LCM
The least common multiple, while seemingly a simple mathematical concept, plays a vital role in various aspects of mathematics and its applications in other fields. Understanding how to calculate the LCM efficiently, using appropriate methods based on the numbers involved, is crucial for problem-solving and making calculations simpler. This article has provided a comprehensive exploration of calculating the LCM of 9 and 12, showcasing various methods and highlighting the broader significance of this fundamental mathematical concept. Mastering the LCM opens doors to a deeper understanding of number theory and its real-world applications.
Latest Posts
Latest Posts
-
Is 35 A Prime Or Composite Number
May 12, 2025
-
How Many Atoms In Calcium Carbonate
May 12, 2025
-
Pictures Of Prokaryotic And Eukaryotic Cells
May 12, 2025
-
Como Se Escribe 180 En Ingles
May 12, 2025
-
Which Of The Following Statements About Secondary Succession Is True
May 12, 2025
Related Post
Thank you for visiting our website which covers about The Lcm Of 9 And 12 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.