The Lcm Of 20 And 25
Juapaving
May 11, 2025 · 5 min read
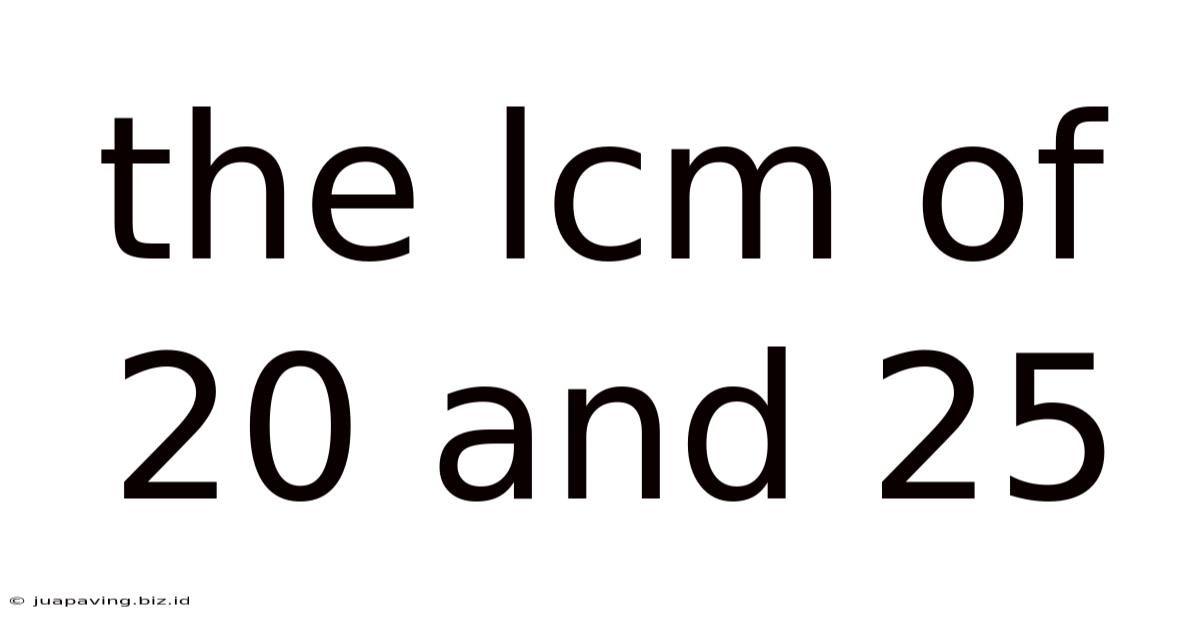
Table of Contents
Finding the Least Common Multiple (LCM) of 20 and 25: A Deep Dive
The least common multiple (LCM) is a fundamental concept in number theory with wide-ranging applications in mathematics, computer science, and even music theory. Understanding how to find the LCM is crucial for various calculations, from simplifying fractions to solving complex algebraic problems. This article will explore the LCM of 20 and 25, demonstrating different methods and providing a comprehensive understanding of the underlying principles. We'll delve into the practical applications and explore how this seemingly simple calculation contributes to more advanced mathematical concepts.
Understanding the Least Common Multiple (LCM)
Before we dive into calculating the LCM of 20 and 25, let's establish a clear understanding of what the LCM actually represents. The least common multiple of two or more integers is the smallest positive integer that is a multiple of all the integers. In simpler terms, it's the smallest number that all the given numbers can divide into evenly.
For example, consider the numbers 2 and 3. The multiples of 2 are 2, 4, 6, 8, 10, 12, and so on. The multiples of 3 are 3, 6, 9, 12, 15, and so on. The common multiples of 2 and 3 are 6, 12, 18, and so on. The least common multiple, therefore, is 6.
This concept extends to more than two numbers as well. Finding the LCM becomes increasingly important as the numbers get larger and the number of integers increases.
Method 1: Listing Multiples
The most straightforward method for finding the LCM, especially for smaller numbers like 20 and 25, is to list the multiples of each number until a common multiple is found.
Let's start with 20:
Multiples of 20: 20, 40, 60, 80, 100, 120, 140, 160, 180, 200...
Now, let's list the multiples of 25:
Multiples of 25: 25, 50, 75, 100, 125, 150, 175, 200...
By comparing the two lists, we can see that the smallest common multiple is 100. Therefore, the LCM of 20 and 25 is 100.
Method 2: Prime Factorization
A more efficient method, especially for larger numbers, is to use prime factorization. This method involves breaking down each number into its prime factors. The prime factors are the prime numbers that multiply together to give the original number. A prime number is a whole number greater than 1 that has only two divisors: 1 and itself.
Let's find the prime factorization of 20 and 25:
- 20: 20 = 2 x 2 x 5 = 2² x 5¹
- 25: 25 = 5 x 5 = 5²
Now, to find the LCM, we take the highest power of each prime factor present in the factorizations:
- The highest power of 2 is 2² = 4
- The highest power of 5 is 5² = 25
Multiply these highest powers together: 4 x 25 = 100
Therefore, the LCM of 20 and 25 using prime factorization is 100. This method is generally preferred for its efficiency, particularly when dealing with larger numbers or a greater number of integers.
Method 3: Using the Greatest Common Divisor (GCD)
The LCM and the greatest common divisor (GCD) are closely related. The GCD is the largest number that divides both integers without leaving a remainder. There's a formula that connects the LCM and GCD:
LCM(a, b) = (|a x b|) / GCD(a, b)
where 'a' and 'b' are the two integers.
First, let's find the GCD of 20 and 25 using the Euclidean algorithm:
- Divide the larger number (25) by the smaller number (20): 25 ÷ 20 = 1 with a remainder of 5.
- Replace the larger number with the smaller number (20) and the smaller number with the remainder (5): 20 ÷ 5 = 4 with a remainder of 0.
- Since the remainder is 0, the GCD is the last non-zero remainder, which is 5.
Now, we can use the formula:
LCM(20, 25) = (20 x 25) / GCD(20, 25) = (500) / 5 = 100
Therefore, using the GCD method, the LCM of 20 and 25 is 100. This method demonstrates the elegant relationship between the LCM and GCD.
Applications of LCM
The LCM has numerous applications across various fields:
-
Fraction Addition and Subtraction: Finding a common denominator when adding or subtracting fractions requires finding the LCM of the denominators.
-
Scheduling Problems: Determining when events will occur simultaneously, such as the meeting of two buses at a bus stop that operate on different schedules, requires finding the LCM of their respective time intervals.
-
Music Theory: The LCM helps in understanding musical intervals and harmonies.
-
Computer Science: The LCM plays a role in algorithms related to time management and resource allocation.
-
Modular Arithmetic: LCM is crucial in solving congruences and problems in modular arithmetic.
Advanced Concepts Related to LCM
The calculation of the LCM extends to more complex scenarios, including:
-
Finding the LCM of more than two numbers: The same principles of prime factorization and the GCD method can be applied to find the LCM of multiple integers.
-
LCM in abstract algebra: The concept of LCM extends into abstract algebra, where it finds applications in ring theory and ideal theory.
-
Relationship with the GCD: The intricate relationship between LCM and GCD is a fundamental concept in number theory, leading to further explorations into modular arithmetic and other number-theoretic properties.
Conclusion
Finding the least common multiple of 20 and 25, while seemingly a simple task, provides a gateway to understanding fundamental concepts in number theory and their applications in diverse fields. Whether using the method of listing multiples, prime factorization, or the GCD method, the result remains consistent: the LCM of 20 and 25 is 100. This understanding forms a building block for more advanced mathematical concepts and problem-solving. Mastering the calculation of the LCM is a valuable skill for anyone seeking a deeper understanding of mathematics and its applications in the real world. The versatility of this seemingly simple calculation showcases its importance in various aspects of mathematical theory and practical problem-solving.
Latest Posts
Latest Posts
-
What Do The Angles In A Hexagon Add Up To
May 13, 2025
-
How Many Gallons In 150 Litres
May 13, 2025
-
What Kind Of Ions Do Metals Form
May 13, 2025
-
Sun Is The Ultimate Source Of Energy On Earth
May 13, 2025
-
Whats The Difference Between A Sea And A Lake
May 13, 2025
Related Post
Thank you for visiting our website which covers about The Lcm Of 20 And 25 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.