The Lcm Of 12 And 9
Juapaving
May 10, 2025 · 5 min read
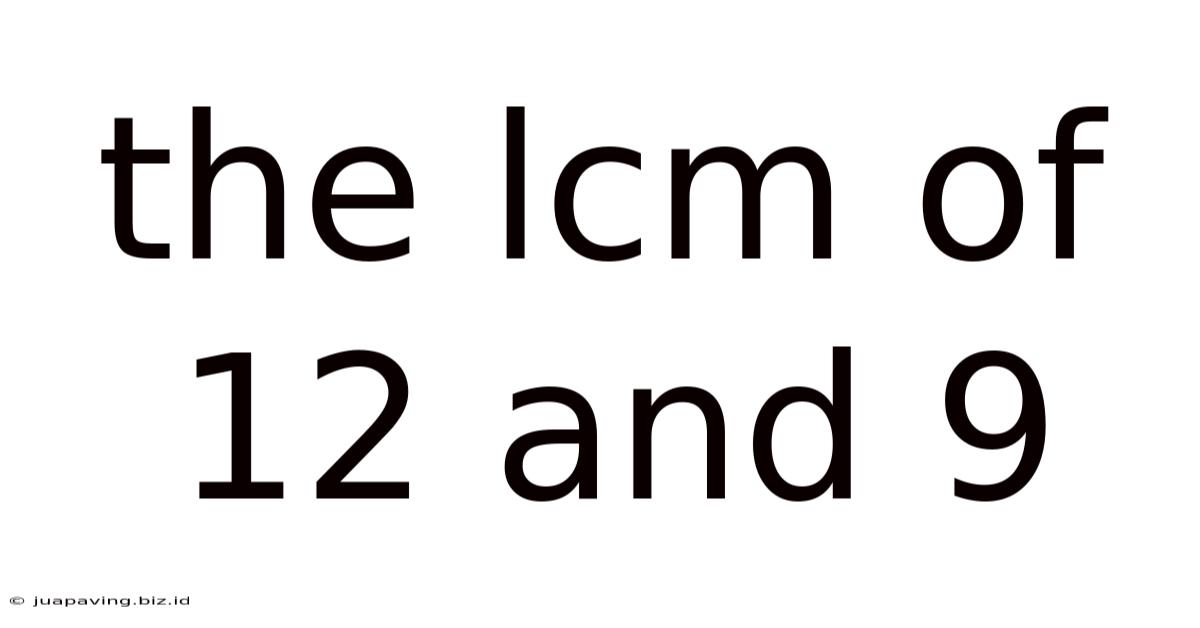
Table of Contents
Finding the LCM of 12 and 9: A Comprehensive Guide
The least common multiple (LCM) is a fundamental concept in mathematics with wide-ranging applications, from simplifying fractions to solving complex problems in number theory and computer science. This article delves deep into calculating the LCM of 12 and 9, exploring various methods and highlighting the significance of this seemingly simple calculation. We'll go beyond a simple answer and explore the underlying concepts, providing a robust understanding of LCM and its practical applications.
Understanding Least Common Multiple (LCM)
Before diving into the calculation, let's solidify our understanding of what the least common multiple actually represents. The LCM of two or more integers is the smallest positive integer that is divisible by all the integers. Think of it as the smallest number that contains all the given numbers as factors. For instance, the multiples of 12 are 12, 24, 36, 48, 60, and so on. The multiples of 9 are 9, 18, 27, 36, 45, and so on. Notice that 36 is the smallest number present in both lists; therefore, 36 is the LCM of 12 and 9.
Why is LCM Important?
The LCM isn't just a theoretical concept; it finds practical applications in numerous areas:
- Fraction Addition and Subtraction: Finding a common denominator when adding or subtracting fractions requires finding the LCM of the denominators. This simplifies the calculation significantly.
- Scheduling and Timing Problems: The LCM is crucial in solving problems related to recurring events, such as determining when two cyclical processes will coincide. For example, if two machines operate on different cycles, the LCM helps determine when they will be operating simultaneously.
- Number Theory and Cryptography: The LCM plays a vital role in advanced mathematical concepts within number theory, which forms the foundation for various encryption methods used in cybersecurity.
- Music Theory: Understanding LCM helps in analyzing musical rhythms and harmonies. Determining the least common multiple of rhythmic patterns helps establish synchronization in musical compositions.
Methods for Finding the LCM of 12 and 9
There are several efficient methods for calculating the LCM. Let's explore the most common approaches:
1. Listing Multiples Method
This method involves listing the multiples of each number until a common multiple is found. While straightforward for smaller numbers, it becomes less efficient with larger numbers.
- Multiples of 12: 12, 24, 36, 48, 60, 72...
- Multiples of 9: 9, 18, 27, 36, 45, 54, 63, 72...
As you can see, the smallest common multiple is 36. Therefore, the LCM(12, 9) = 36.
2. Prime Factorization Method
This method leverages the prime factorization of each number. Prime factorization is the process of expressing a number as a product of its prime factors (numbers divisible only by 1 and themselves).
- Prime factorization of 12: 2² × 3
- Prime factorization of 9: 3²
To find the LCM using prime factorization:
- Identify the highest power of each prime factor present in the factorizations. In this case, we have 2² and 3².
- Multiply these highest powers together. This gives us 2² × 3² = 4 × 9 = 36.
Therefore, the LCM(12, 9) = 36. This method is generally more efficient for larger numbers as it avoids the need to list out extensive multiples.
3. Greatest Common Divisor (GCD) Method
The LCM and GCD (greatest common divisor) are closely related. The product of the LCM and GCD of two numbers is equal to the product of the two numbers. This relationship provides another method for finding the LCM.
First, let's find the GCD of 12 and 9 using the Euclidean algorithm:
- Divide the larger number (12) by the smaller number (9). The remainder is 3.
- Replace the larger number with the smaller number (9) and the smaller number with the remainder (3).
- Repeat the process: 9 divided by 3 has a remainder of 0.
- The last non-zero remainder is the GCD, which is 3.
Now, we can use the relationship: LCM(a, b) = (a × b) / GCD(a, b)
LCM(12, 9) = (12 × 9) / 3 = 108 / 3 = 36
Therefore, the LCM(12, 9) = 36. This method is particularly useful when dealing with larger numbers, where finding prime factorizations can be computationally intensive.
Applications of LCM(12, 9) = 36
Let's illustrate the practical application of the LCM(12, 9) = 36 with some examples:
Example 1: Fraction Addition
Add the fractions 5/12 and 2/9.
To add these fractions, we need a common denominator, which is the LCM of 12 and 9. We already know this is 36.
5/12 = (5 × 3) / (12 × 3) = 15/36 2/9 = (2 × 4) / (9 × 4) = 8/36
15/36 + 8/36 = 23/36
Example 2: Scheduling
Two machines operate on cycles of 12 hours and 9 hours respectively. When will they both be operating simultaneously again after they start at the same time?
The answer is determined by the LCM of 12 and 9, which is 36 hours. Both machines will operate simultaneously again after 36 hours.
Expanding the Concept: LCM of More Than Two Numbers
The methods described above can be extended to find the LCM of more than two numbers. For the prime factorization method, you simply consider all the prime factors and their highest powers across all numbers. For the GCD method, you can use iterative approaches, finding the LCM of two numbers at a time and then finding the LCM of the result with the next number, and so on.
Conclusion
Finding the LCM of 12 and 9, while seemingly a simple calculation, provides a gateway to understanding a fundamental mathematical concept with diverse applications. Through exploring different methods, from listing multiples to employing prime factorization and the GCD relationship, we've not only determined the LCM to be 36, but also grasped the underlying principles and practical significance of this important mathematical tool. The ability to efficiently calculate the LCM is crucial in various fields, highlighting the importance of mastering this fundamental concept. Understanding the LCM is not just about solving mathematical problems; it's about gaining a deeper understanding of the structure and relationships within numbers, a foundation for more advanced mathematical explorations.
Latest Posts
Latest Posts
-
Oxidation Number For S In So2
May 10, 2025
-
Molecules Need A Carrier Protein Because
May 10, 2025
-
The Rate Of Doing Work Is Called
May 10, 2025
-
Why Are Covalent Bonds Soluble In Water
May 10, 2025
-
Can Elements Be Separated By Physical Means
May 10, 2025
Related Post
Thank you for visiting our website which covers about The Lcm Of 12 And 9 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.