The Distance Around A Figure Is Called
Juapaving
Mar 29, 2025 · 5 min read
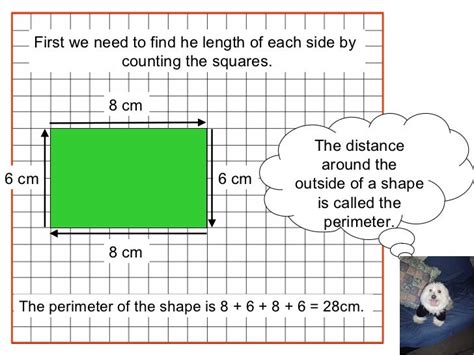
Table of Contents
The Distance Around a Figure is Called: Perimeter, Circumference, and More
The distance around a figure is a fundamental concept in geometry with various names depending on the shape. While the most common term is perimeter, other terms like circumference and arc length are used for specific shapes and parts of shapes. This comprehensive guide will delve into the precise definitions, calculations, and real-world applications of these concepts. We'll explore how understanding these measurements can be crucial in diverse fields, from architecture and engineering to everyday tasks.
Understanding Perimeter
The perimeter is the total distance around the outside of a two-dimensional (2D) shape. It's the sum of all the lengths of the sides of a polygon. Think of it as walking around the edge of a field; the total distance you walk is the perimeter.
Calculating Perimeter:
The method for calculating perimeter depends on the shape:
-
Regular Polygons: For regular polygons (polygons with all sides and angles equal), the perimeter is simply the side length multiplied by the number of sides. For example, a square with a side length of 5 cm has a perimeter of 5 cm * 4 = 20 cm. An equilateral triangle with sides of 7 inches has a perimeter of 7 inches * 3 = 21 inches.
-
Irregular Polygons: For irregular polygons (polygons with unequal sides), you need to measure the length of each side and then add them together. For example, if a polygon has sides of 3, 5, 7, and 2 units, the perimeter is 3 + 5 + 7 + 2 = 17 units.
-
Circles and Perimeter Analogue (Circumference): Circles don't have sides in the traditional sense. Instead, the distance around a circle is called its circumference. The formula for calculating the circumference (C) is:
C = 2πr or C = πd
Where:
- 'r' is the radius of the circle (the distance from the center to any point on the circle).
- 'd' is the diameter of the circle (twice the radius).
- 'π' (pi) is a mathematical constant, approximately equal to 3.14159.
Real-world Applications of Perimeter:
Understanding perimeter is crucial in many real-world scenarios:
-
Construction and Architecture: Architects and builders use perimeter calculations to determine the amount of fencing, materials, or landscaping needed for a property or building.
-
Landscaping: Determining the amount of fencing required for a yard or garden.
-
Sports: The perimeter of a sports field (football field, running track, etc.) is essential for layout and game play.
-
Framing Pictures: Knowing the perimeter helps determine the amount of frame needed for a picture.
-
Sewing and Crafts: Calculating the perimeter of fabric pieces is vital in sewing and crafting projects.
Understanding Circumference
As mentioned earlier, circumference is the specific term for the perimeter of a circle. It's a crucial concept in various fields, particularly those involving circular motion or areas.
Calculating Circumference:
The formulas mentioned earlier, C = 2πr and C = πd, are fundamental to circumference calculations. The choice of which formula to use depends on whether the radius or the diameter is known.
Real-world Applications of Circumference:
Circumference finds application in diverse fields:
-
Engineering: Calculating the circumference of wheels, pulleys, and gears is essential in mechanical engineering.
-
Astronomy: The circumference of planets and stars is a fundamental parameter in astrophysics.
-
Manufacturing: Circumference is vital in the production of circular parts and components.
-
Wheel Speed: Knowing the circumference of a wheel helps calculate distance traveled based on the number of rotations.
-
Track and Field: The circumference of a running track directly impacts race distances.
Arc Length: A Part of the Perimeter
When dealing with only a portion of a circle's perimeter, we use the term arc length. An arc is a segment of the circle's circumference.
Calculating Arc Length:
The formula for arc length (s) is:
s = rθ
Where:
- 'r' is the radius of the circle.
- 'θ' (theta) is the central angle subtended by the arc (in radians). To convert degrees to radians, use the formula: Radians = (Degrees * π) / 180.
Real-world Applications of Arc Length:
Arc length has significant applications in:
-
Cartography: Calculating distances on the Earth's surface (which is approximately spherical).
-
Circular Motion: Determining the distance traveled by a point moving along a circular path.
-
Engineering Design: Calculating the length of curved sections in designs.
-
Clocks and Watches: The arc length relates to the movement of the hands.
Other Related Concepts
While perimeter, circumference, and arc length are the primary ways to describe the distance around a figure, other related geometric concepts deserve mention:
-
Diameter: The distance across a circle through its center.
-
Radius: The distance from the center of a circle to any point on the circle.
-
Chord: A line segment whose endpoints lie on the circle.
-
Sector: The region bounded by two radii and an arc of a circle.
-
Segment: The region bounded by a chord and an arc of a circle.
Advanced Concepts and Applications
The calculation of perimeter, circumference, and arc length forms the basis for many more complex geometric concepts and applications. For instance:
-
Calculus: The concept of arc length extends into calculus, where it's used to calculate the length of curves defined by functions.
-
Surface Area: The concept of perimeter is foundational in calculating the surface area of three-dimensional (3D) shapes, especially those with curved surfaces. The surface area of a cylinder, for example, incorporates the circumference of its circular bases.
-
Volume: The volume of certain 3D shapes like cylinders and cones incorporates the circumference and radius.
-
Complex Shapes: For irregular or complex shapes, numerical methods such as integration or approximation techniques might be necessary to estimate the perimeter accurately.
Conclusion
Understanding the distance around a figure – whether it's the perimeter of a polygon, the circumference of a circle, or the arc length of a circular segment – is fundamental to various fields. From the construction of buildings to the design of machines, the calculation and application of these geometric concepts are essential for solving real-world problems. Mastering these concepts provides a solid foundation for further explorations in mathematics and its practical applications. By understanding these concepts, you're equipped to tackle a wide range of challenges and achieve greater precision and accuracy in your calculations. The seemingly simple idea of measuring the distance around a shape has far-reaching implications across diverse disciplines and everyday life.
Latest Posts
Latest Posts
-
In Glycolysis There Is A Net Gain Of Atp
Mar 31, 2025
-
The Clavicle Articulates With The Sternum And The Scapula
Mar 31, 2025
-
Is Oxygen A Metal Nonmetal Or Metalloid
Mar 31, 2025
-
Keyboard Is A Hardware Or Software
Mar 31, 2025
-
Is 45 A Multiple Of 9
Mar 31, 2025
Related Post
Thank you for visiting our website which covers about The Distance Around A Figure Is Called . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
