Sum Of Interior Angles Of A Nonagon
Juapaving
Apr 07, 2025 · 5 min read
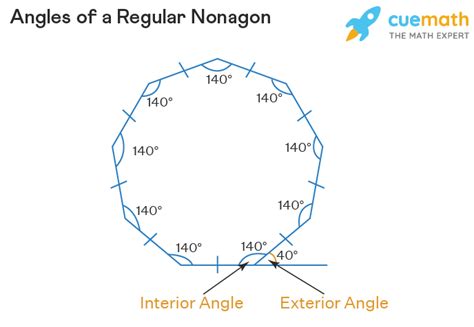
Table of Contents
The Sum of Interior Angles of a Nonagon: A Comprehensive Guide
The sum of the interior angles of a polygon, a closed two-dimensional shape with straight sides, is a fundamental concept in geometry. Understanding this concept is crucial for solving various geometric problems, from calculating individual angles in complex shapes to tackling more advanced topics like trigonometry and calculus. This article dives deep into the sum of interior angles of a nonagon, a nine-sided polygon, exploring different methods of calculation, providing practical examples, and extending the concept to other polygons.
Understanding Polygons and Their Angles
Before we focus specifically on nonagons, let's establish a firm understanding of polygons in general. A polygon is defined by its number of sides, and this number directly impacts the sum of its interior angles. Some common polygons include:
- Triangle (3 sides): The simplest polygon, with an interior angle sum of 180°.
- Quadrilateral (4 sides): A four-sided polygon, like squares and rectangles, with an interior angle sum of 360°.
- Pentagon (5 sides): A five-sided polygon, with an interior angle sum of 540°.
- Hexagon (6 sides): A six-sided polygon, often found in nature like honeycombs, with an interior angle sum of 720°.
- Heptagon (7 sides): A seven-sided polygon, also known as a septagon.
- Octagon (8 sides): An eight-sided polygon, frequently seen in architecture.
- Nonagon (9 sides): Our focus for this article, a nine-sided polygon.
- Decagon (10 sides): A ten-sided polygon.
- And so on…
Calculating the Sum of Interior Angles of a Nonagon
There are several ways to calculate the sum of the interior angles of a nonagon. Let's explore the most common and effective methods:
Method 1: Using the Formula
The most efficient method utilizes a general formula that works for any polygon, regardless of the number of sides. The formula is:
Sum of interior angles = (n - 2) × 180°
Where 'n' represents the number of sides of the polygon.
For a nonagon (n = 9), the calculation is straightforward:
Sum of interior angles = (9 - 2) × 180° = 7 × 180° = 1260°
Therefore, the sum of the interior angles of any nonagon is always 1260°.
Method 2: Triangulation
This method involves dividing the nonagon into triangles. You can do this by drawing lines from a single vertex to all other non-adjacent vertices. This will divide the nonagon into seven triangles. Since the sum of the interior angles of a triangle is 180°, the total sum of the interior angles of the nonagon is simply 7 × 180° = 1260°. This method visually demonstrates the connection between the number of sides and the sum of interior angles.
Method 3: Exterior Angles
While less commonly used for finding the sum of interior angles, understanding the relationship between interior and exterior angles is valuable. The sum of the exterior angles of any polygon is always 360°. Each exterior angle is supplementary to its corresponding interior angle (they add up to 180°). While not directly calculating the sum of interior angles, this approach provides an alternative perspective and reinforces fundamental geometric principles.
Regular vs. Irregular Nonagons
It's important to distinguish between regular and irregular nonagons:
-
Regular Nonagon: A nonagon with all sides equal in length and all angles equal in measure. Each interior angle of a regular nonagon measures 1260°/9 = 140°.
-
Irregular Nonagon: A nonagon where the sides and angles are not all equal. The sum of the interior angles remains 1260°, but the individual angles will vary.
Practical Applications and Examples
The concept of the sum of interior angles of a nonagon (and polygons in general) has numerous applications in various fields:
-
Architecture and Construction: Designing buildings, bridges, and other structures often involves precise angle calculations to ensure stability and aesthetics. Understanding polygon angles is crucial for creating accurate blueprints and ensuring structural integrity.
-
Computer Graphics and Game Development: Creating realistic 3D models and environments requires a deep understanding of geometry, including polygon angles. Accurate angle calculations are critical for rendering realistic shapes and textures.
-
Cartography: Mapping and surveying often involve working with polygons to represent land areas and calculate distances. Understanding polygon angles is essential for accurately representing geographical features.
-
Engineering: Many engineering projects, such as designing gears, require precise calculations of angles, including the interior angles of polygons like nonagons.
Example 1: Imagine a regular nonagon-shaped tile. Each interior angle measures 140°. This information is critical for determining how these tiles can fit together seamlessly to cover a surface.
Example 2: Consider an irregular nonagon representing a piece of land. Knowing that the sum of its interior angles is 1260° allows surveyors to check the accuracy of their measurements. If the sum of measured angles significantly deviates from 1260°, it indicates an error in the surveying process.
Extending the Concept to Other Polygons
The principles discussed for nonagons apply to all polygons. The formula (n - 2) × 180° is universally applicable, providing a powerful tool for calculating the sum of interior angles for any polygon with 'n' sides. This understanding forms the foundation for more advanced geometric concepts.
Conclusion: Mastering Polygon Angles
Understanding the sum of interior angles of a nonagon, and polygons in general, is essential for various applications across numerous disciplines. The formula (n - 2) × 180° provides a simple yet powerful method for calculating this sum, while triangulation offers a visual approach to understanding the underlying principles. Whether you're an architect designing a building, a game developer creating a virtual world, or simply a student learning geometry, mastering the concept of polygon angles is a valuable skill. Remember, the sum of interior angles of a nonagon is always 1260°, a fundamental fact that opens doors to more complex geometric explorations. This constant, regardless of the specific nonagon's shape (regular or irregular), highlights the elegance and power of geometric principles. By comprehending these concepts thoroughly, you equip yourself with the knowledge to tackle various geometric challenges with confidence and precision.
Latest Posts
Latest Posts
-
What Are Organisms That Make Their Own Food
Apr 09, 2025
-
Least Common Multiple Of 24 And 30
Apr 09, 2025
-
What Is The Least Common Multiple Of 10 And 3
Apr 09, 2025
-
How Many Cm In 2 M
Apr 09, 2025
-
Why Is A Production Possibility Curve Concave
Apr 09, 2025
Related Post
Thank you for visiting our website which covers about Sum Of Interior Angles Of A Nonagon . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.