Sin 60 Cos 30 - Cos 60 Sin 30
Juapaving
May 10, 2025 · 4 min read
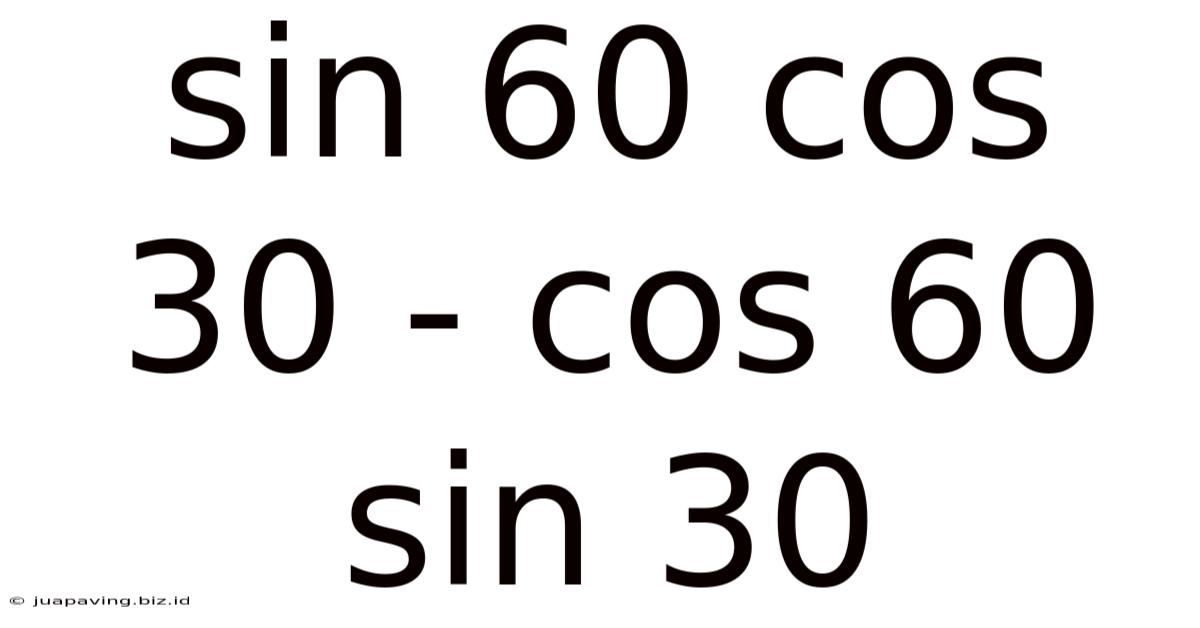
Table of Contents
Decoding sin 60 cos 30 - cos 60 sin 30: A Deep Dive into Trigonometric Identities
The expression sin 60 cos 30 - cos 60 sin 30 might seem daunting at first glance, particularly for those less familiar with trigonometry. However, this seemingly complex expression is actually a straightforward application of a fundamental trigonometric identity – the difference formula for sine. This article will not only solve the expression but also explore the underlying principles, provide practical examples, and delve into the broader applications of trigonometric identities in various fields.
Understanding the Trigonometric Identity: sin(A - B)
The core of solving sin 60 cos 30 - cos 60 sin 30 lies in recognizing its connection to the sine subtraction formula:
sin(A - B) = sin A cos B - cos A sin B
Notice the striking similarity between the given expression and the right-hand side of this identity. By comparing the two, we can identify:
- A = 60°
- B = 30°
Therefore, our expression simplifies to:
sin (60° - 30°) = sin 30°
Calculating the Result: sin 30°
Now, we just need to determine the value of sin 30°. This is a standard trigonometric value that's frequently encountered. The sine function represents the ratio of the opposite side to the hypotenuse in a right-angled triangle. In a 30-60-90 triangle (a special right triangle), the ratio is:
sin 30° = 1/2 or 0.5
Therefore, sin 60 cos 30 - cos 60 sin 30 = 1/2 or 0.5
Beyond the Calculation: Exploring Trigonometric Identities
While we've successfully solved the given expression, the significance extends beyond a single calculation. Understanding and applying trigonometric identities is crucial for:
1. Simplifying Complex Expressions:
Trigonometric identities provide tools to simplify complex expressions, making them easier to manipulate and analyze. This is especially valuable in calculus, physics, and engineering, where complex trigonometric functions are common.
2. Solving Trigonometric Equations:
Many trigonometric equations are unsolvable directly. However, by strategically applying identities, we can transform these equations into simpler, more manageable forms, leading to solutions.
3. Proving Other Identities:
Trigonometric identities are building blocks for proving other, more complex identities. By systematically applying known identities, we can demonstrate the validity of new relationships between trigonometric functions.
4. Applications in various fields:
- Physics: Trigonometry is fundamental to many areas of physics, including mechanics, optics, and wave phenomena. Identities are crucial for simplifying and solving equations related to these topics.
- Engineering: Engineers use trigonometry extensively in structural analysis, surveying, and signal processing, relying heavily on identities to solve complex problems.
- Computer graphics: Computer graphics utilizes trigonometry for rotations, transformations, and projections. Efficient algorithms often rely on optimized trigonometric identities.
- Navigation: Navigation systems rely on trigonometric calculations to determine distances, bearings, and positions, using identities for simplification and accuracy.
Illustrative Examples of Trigonometric Identities:
Let's explore some further examples to solidify our understanding:
1. The Cosine Subtraction Formula:
Similar to the sine subtraction formula, we have a cosine subtraction formula:
cos(A - B) = cos A cos B + sin A sin B
This identity can be used to simplify expressions involving cosine functions of differences.
2. The Sine Addition Formula:
The sine addition formula is closely related to the subtraction formula:
sin(A + B) = sin A cos B + cos A sin B
This formula enables us to express the sine of a sum of angles in terms of the sines and cosines of individual angles.
3. The Cosine Addition Formula:
Similarly, we have the cosine addition formula:
cos(A + B) = cos A cos B - sin A sin B
This complements the cosine subtraction formula and allows for similar manipulations.
Practical Applications: Real-world Scenarios
Consider a scenario in surveying. You need to determine the distance across a river. You can measure the distance along one bank and the angles to a point on the opposite bank. By using the sine or cosine rules (which are derived from trigonometric identities), you can calculate the distance across the river.
Another example involves the calculation of the resultant force of two vectors. If you know the magnitude and direction of two forces acting on an object, you can use trigonometric identities to determine the net force and its direction. This is critical in structural engineering and physics.
Conclusion: The Power of Trigonometric Identities
The seemingly simple expression sin 60 cos 30 - cos 60 sin 30 serves as a gateway to the profound world of trigonometric identities. Understanding and applying these identities is essential for simplifying complex expressions, solving equations, and tackling real-world problems across diverse fields. Mastering these fundamental principles opens doors to advanced concepts in mathematics, science, and engineering, empowering you to solve complex challenges with elegance and precision. Remember to practice regularly to build a strong intuition and proficiency with trigonometric identities. The more you practice, the more natural and intuitive their application will become.
Latest Posts
Latest Posts
-
The Eye And Ear Are Part Of Which System
May 10, 2025
-
Which Of The Following Geometric Objects Occupy Two Dimensions
May 10, 2025
-
Portion Of The Retina That Contains No Photoreceptors
May 10, 2025
-
Which Of The Following Compounds Is Most Acidic
May 10, 2025
-
Whats The Prime Factorization Of 50
May 10, 2025
Related Post
Thank you for visiting our website which covers about Sin 60 Cos 30 - Cos 60 Sin 30 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.