Simplify The Square Root Of 99
Juapaving
May 12, 2025 · 5 min read
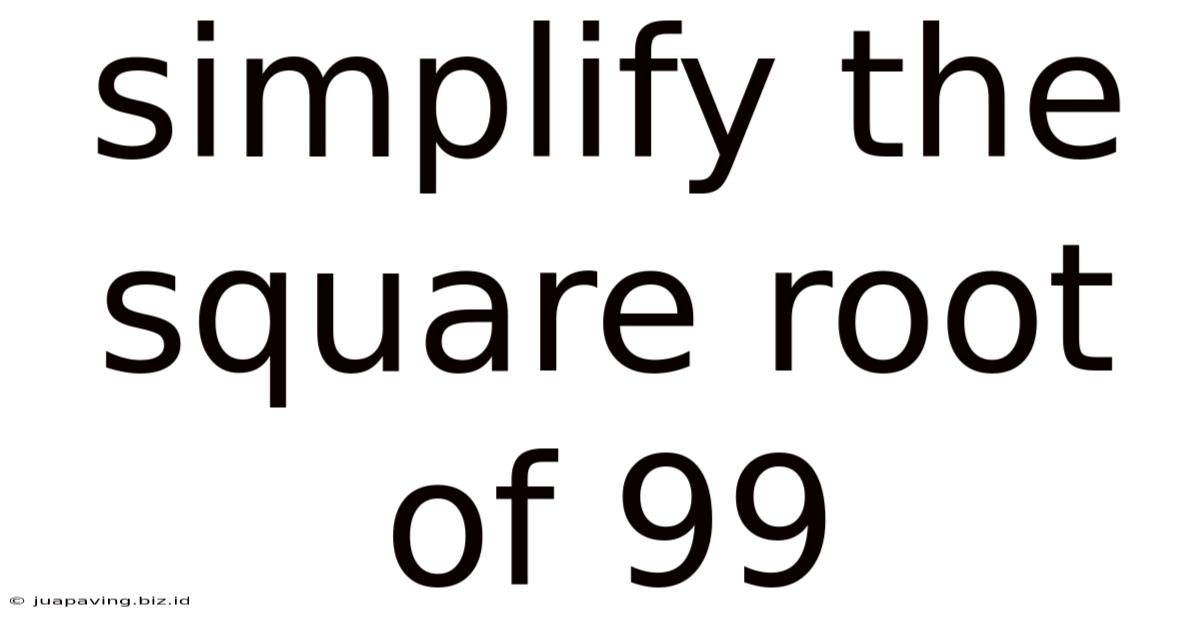
Table of Contents
Simplifying the Square Root of 99: A Comprehensive Guide
The seemingly simple task of simplifying the square root of 99 presents a fantastic opportunity to delve into the fundamentals of square roots, prime factorization, and radical simplification. This comprehensive guide will walk you through the process step-by-step, exploring various methods and providing a deeper understanding of the underlying mathematical principles. We'll also touch upon practical applications and common misconceptions.
Understanding Square Roots
Before we tackle the square root of 99, let's refresh our understanding of square roots. A square root of a number is a value that, when multiplied by itself, equals the original number. For example, the square root of 25 (√25) is 5 because 5 x 5 = 25. Square roots can be either rational (expressed as a simple fraction) or irrational (cannot be expressed as a simple fraction, like √2).
Perfect Squares and Non-Perfect Squares
A perfect square is a number that results from squaring an integer. Examples include 4 (2 x 2), 9 (3 x 3), 16 (4 x 4), and so on. Numbers that are not perfect squares, like 99, have square roots that are irrational. This means their decimal representation continues infinitely without repeating.
Prime Factorization: The Key to Simplification
Simplifying a square root involves finding its prime factorization. Prime factorization is the process of expressing a number as the product of its prime factors – numbers that are only divisible by 1 and themselves (e.g., 2, 3, 5, 7, 11, etc.).
To simplify √99, we first find the prime factorization of 99:
- 99 is divisible by 3 (99 ÷ 3 = 33)
- 33 is also divisible by 3 (33 ÷ 3 = 11)
- 11 is a prime number.
Therefore, the prime factorization of 99 is 3 x 3 x 11, or 3² x 11.
Simplifying the Square Root
Now that we have the prime factorization of 99 (3² x 11), we can simplify the square root:
√99 = √(3² x 11)
Using the property of square roots that √(a x b) = √a x √b, we can rewrite this as:
√99 = √3² x √11
Since √3² = 3, we get:
√99 = 3√11
Therefore, the simplified form of √99 is 3√11. This means that 3√11, when multiplied by itself, equals 99.
Alternative Methods and Visual Representations
While prime factorization is the most efficient method, let's explore alternative approaches to help solidify your understanding:
Using a Factor Tree
A factor tree is a visual tool to break down a number into its prime factors. Start with 99, find two factors (like 9 and 11), then break down those factors further until you only have prime numbers left. This will lead you to the same 3² x 11 factorization.
Repeated Division
Another approach involves repeatedly dividing the number by its prime factors until you reach 1. Start by dividing 99 by 3, then the result (33) by 3, and finally 11 (which is prime) by 11. The prime factors you used (3, 3, and 11) give you the same factorization.
Practical Applications and Real-World Examples
Simplifying square roots isn't just an abstract mathematical exercise; it has practical applications in various fields:
-
Geometry: Calculating the length of the diagonal of a square or rectangle often involves simplifying square roots. For instance, finding the diagonal of a square with sides of length 3√11 would require working with simplified square roots.
-
Physics: Many physics equations involve square roots, particularly those dealing with vectors and motion. Simplifying square roots is essential for obtaining accurate and efficient calculations.
-
Engineering: Engineering designs and calculations frequently involve simplifying square roots to ensure precision and efficiency in design processes. Structural calculations or electrical circuit analysis often require handling of irrational numbers.
-
Computer Graphics: Representing points and distances on a 2D or 3D plane frequently utilizes square roots. Simplifying square roots makes the calculations more efficient in computer graphics.
Common Mistakes to Avoid
When simplifying square roots, be mindful of these common pitfalls:
-
Incorrect prime factorization: Ensure you accurately identify all prime factors of the number. Missing a prime factor will lead to an incorrect simplification.
-
Confusing √a + √b with √(a+b): Remember that √a + √b ≠ √(a+b). These are distinct mathematical expressions and cannot be simplified together directly.
-
Ignoring simplification after prime factorization: Once you find the prime factorization, you must simplify the square root appropriately by taking out perfect squares.
-
Approximating too early: Avoid approximating the decimal value of the square root before simplifying. Simplify the radical first to get the most accurate and simplified result.
Advanced Concepts and Extensions
While simplifying √99 is a fundamental exercise, it provides a foundation for more complex mathematical concepts:
-
Complex Numbers: The concept extends to simplifying square roots of negative numbers, introducing the imaginary unit "i" (√-1) and leading to the realm of complex numbers.
-
Higher-Order Roots: The principles of prime factorization and simplification apply equally to cube roots (∛), fourth roots (∜), and roots of any order.
-
Solving Quadratic Equations: Simplifying square roots is crucial in solving quadratic equations using the quadratic formula. The formula involves a square root term that often needs simplification.
-
Calculus: Derivatives and integrals frequently involve manipulating expressions containing square roots, requiring a solid understanding of simplification techniques.
Conclusion: Mastering Square Root Simplification
Mastering the simplification of square roots like √99 is essential for success in various mathematical and scientific fields. By understanding prime factorization and applying the appropriate rules, we can efficiently simplify seemingly complex expressions, leading to accurate and concise results. Remember to practice regularly, paying close attention to potential pitfalls and exploring different methods to reinforce your understanding. Through consistent practice and attention to detail, you will confidently navigate the world of square root simplification.
Latest Posts
Latest Posts
-
Chemical Reaction Of Magnesium And Oxygen
May 12, 2025
-
How Many Feet Is 26 In
May 12, 2025
-
Which Answer Choice Contains All The Factors Of 10
May 12, 2025
-
When Hydrogen And Oxygen Combine And Form Water Water Is
May 12, 2025
-
Five Letter Words Ending In I N
May 12, 2025
Related Post
Thank you for visiting our website which covers about Simplify The Square Root Of 99 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.