Sample Space Of Flipping A Coin 3 Times
Juapaving
Apr 07, 2025 · 5 min read
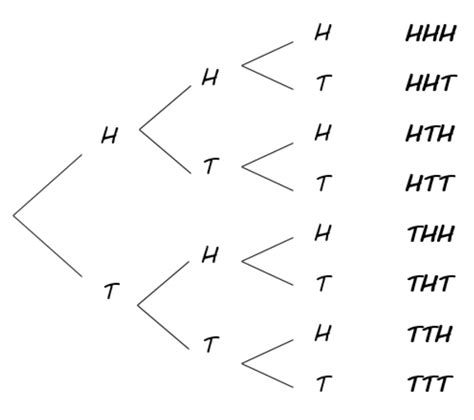
Table of Contents
Delving Deep into the Sample Space of Flipping a Coin Three Times
Flipping a coin is a seemingly simple act, yet it holds a surprising depth when we delve into the possibilities of multiple flips. This article will explore the sample space of flipping a coin three times, examining its structure, calculating probabilities, and extending the concepts to more complex scenarios. We'll uncover how understanding sample spaces is fundamental to probability theory and its applications in various fields.
Understanding Sample Space
In probability, the sample space (often denoted as S) represents the set of all possible outcomes of a random experiment. When flipping a single coin, the sample space is straightforward: {Heads, Tails}. However, as we increase the number of coin flips, the sample space grows significantly, becoming more complex to visualize and analyze.
The Three Coin Flips Experiment: Visualizing the Possibilities
Let's consider the experiment of flipping a fair coin three times. Each flip is independent of the others, meaning the outcome of one flip doesn't influence the outcome of any other flip. This independence is crucial for calculating probabilities.
To visualize the sample space, we can use a tree diagram. This diagram visually branches out, showing all possible sequences of heads (H) and tails (T) after each flip:
Flip 1 Flip 2 Flip 3
/ \ / \ / \
H T H T H T
/ \ / \ / \ / \ / \ / \
HH HT TH TT HH HT TH TT HH HT TH TT
This tree diagram clearly shows eight possible outcomes. These outcomes represent the complete sample space for flipping a coin three times. We can list them as:
- S = {HHH, HHT, HTH, HTT, THH, THT, TTH, TTT}
This set, S, contains all possible sequences of three coin flips. Each element in the set is a unique outcome of the experiment.
Calculating Probabilities within the Sample Space
With the sample space defined, we can now calculate probabilities of specific events. Assuming a fair coin (equal probability of heads and tails), each of the eight outcomes in S has an equal probability of occurring. The probability of any single outcome is 1/8 or 12.5%.
Let's consider some examples:
-
Probability of getting exactly two heads: There are three outcomes with exactly two heads: HHT, HTH, THH. Therefore, the probability is 3/8.
-
Probability of getting at least one head: This includes all outcomes except TTT. There are seven such outcomes. Therefore, the probability is 7/8.
-
Probability of getting heads on the first flip: This includes HHH, HHT, HTH, HTT. The probability is 4/8, which simplifies to 1/2. This intuitively makes sense, as the probability of heads on any single flip is 1/2.
Extending the Concept: More Than Three Flips
The principles discussed above can be extended to a greater number of coin flips. For 'n' coin flips, the size of the sample space is 2<sup>n</sup>. This is because for each flip, there are two possibilities (H or T), and these possibilities multiply for each subsequent flip.
For example:
- Four coin flips: 2<sup>4</sup> = 16 possible outcomes
- Five coin flips: 2<sup>5</sup> = 32 possible outcomes
- Ten coin flips: 2<sup>10</sup> = 1024 possible outcomes
As the number of flips increases, the sample space grows exponentially. While manually creating tree diagrams becomes impractical, the fundamental concept of the sample space remains the same: a complete set of all possible outcomes.
Using Combinatorics for Larger Sample Spaces
For a larger number of coin flips, using combinatorics simplifies probability calculations. Combinatorics is the branch of mathematics that deals with counting and arranging objects.
For example, to calculate the probability of getting exactly k heads in n coin flips, we use the binomial coefficient:
P(k heads in n flips) = (n choose k) * (1/2)<sup>k</sup> * (1/2)<sup>(n-k)</sup> = (n choose k) * (1/2)<sup>n</sup>
Where (n choose k) is the binomial coefficient, calculated as:
(n choose k) = n! / (k! * (n-k)!)
This formula significantly simplifies the calculation of probabilities for a large number of coin flips, eliminating the need to enumerate all possible outcomes.
Applications in Real-World Scenarios
The principles of sample spaces and probability calculations, exemplified by the coin-flipping experiment, have far-reaching applications:
- Quality Control: In manufacturing, understanding sample spaces helps determine the probability of defective items in a batch.
- Medical Trials: Sample spaces are crucial in analyzing the effectiveness of new treatments, considering various outcomes and their probabilities.
- Financial Modeling: Probability models, built upon sample spaces, are used to assess risk in investment strategies.
- Genetics: Sample spaces help model the inheritance of genes and predict the probability of offspring inheriting certain traits.
- Game Theory: Understanding sample spaces is fundamental to analyzing the probability of winning or losing in various games of chance.
Beyond Fair Coins: Biased Coins and Conditional Probabilities
The examples above assume a fair coin. However, the concept of sample space extends to biased coins, where the probability of heads (P(H)) is not equal to the probability of tails (P(T)). In this case, the probability of each outcome in the sample space needs to be adjusted accordingly.
Moreover, we can explore conditional probabilities. For instance, what is the probability of getting three heads given that the first flip was heads? This involves considering a subset of the sample space and recalculating probabilities based on this condition.
Conclusion: The Power of Sample Spaces
The seemingly simple act of flipping a coin three times opens a window into the fascinating world of probability and sample spaces. Understanding the structure of the sample space, calculating probabilities, and extending these concepts to more complex scenarios are essential skills in various fields. The principles discussed here—from tree diagrams to combinatorics and the consideration of biased coins—provide a solid foundation for tackling more advanced probability problems and applying these concepts to real-world challenges. Mastering the sample space is the key to unlocking the power of probability. By understanding and applying these concepts, you can develop a deeper understanding of uncertainty and make more informed decisions in various aspects of life. From the simplest coin flip to complex scientific models, sample spaces serve as the bedrock for quantifying and managing uncertainty.
Latest Posts
Latest Posts
-
The Image Produced By A Convex Lens Depends Upon
Apr 08, 2025
-
What Percentage Of 25 Is 4
Apr 08, 2025
-
How Much Protons Does Sodium Have
Apr 08, 2025
-
How Many Hours Is 10 Minutes
Apr 08, 2025
-
Why Is It Difficult To Walk On Sand
Apr 08, 2025
Related Post
Thank you for visiting our website which covers about Sample Space Of Flipping A Coin 3 Times . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.