Points Lie On The Same Line
Juapaving
Apr 06, 2025 · 6 min read
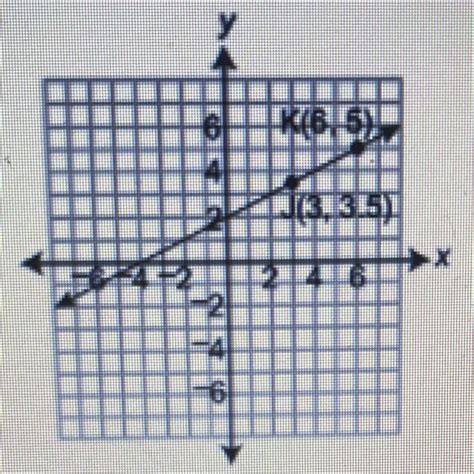
Table of Contents
Points Lying on the Same Line: A Comprehensive Guide to Collinearity
Collinearity, the state of points lying on the same straight line, is a fundamental concept in geometry with far-reaching applications in various fields, from computer graphics and spatial analysis to physics and engineering. Understanding collinearity involves not just recognizing when points are collinear but also mastering the techniques to determine collinearity and its implications. This comprehensive guide delves into the intricacies of collinear points, exploring different approaches to identify them and highlighting their importance in various disciplines.
Defining Collinearity: What Does it Mean?
At its core, collinearity refers to the property of three or more points lying on a single straight line. These points share a common line of intersection. While two points always define a line, the presence of a third (or more) point on that same line signifies collinearity. This seemingly simple concept forms the basis for numerous geometric theorems, algorithms, and real-world applications.
Visualizing Collinearity: Imagine three pins stuck on a corkboard. If you can draw a single straight line that passes through all three pins without deviation, then the pins represent collinear points. Conversely, if the pins require multiple lines to connect them all, they are non-collinear.
Methods for Determining Collinearity
Several methods exist to ascertain whether a set of points is collinear. The choice of method often depends on the context and the format of the data representing the points.
1. Using the Slope Formula
This is a straightforward approach, particularly effective when dealing with two-dimensional points. The slope between any two points (x1, y1) and (x2, y2) is calculated as (y2 - y1) / (x2 - x1). If multiple pairs of points share the same slope, it strongly suggests collinearity. However, this method has limitations:
- Vertical Lines: The slope of a vertical line is undefined, making this method inapplicable for such cases.
- Computational Errors: Small rounding errors in calculations could lead to slightly different slopes, resulting in false negatives (misclassifying collinear points as non-collinear).
Example: Consider points A(1, 2), B(3, 4), and C(5, 6). The slope between A and B is (4-2)/(3-1) = 1. The slope between B and C is (6-4)/(5-3) = 1. Since the slopes are equal, points A, B, and C are collinear.
2. Using the Area of a Triangle
A more robust method involves calculating the area of the triangle formed by three points. If the area is zero, the points are collinear. The area can be calculated using the determinant formula:
Area = 0.5 * |x1(y2 - y3) + x2(y3 - y1) + x3(y1 - y2)|
Where (x1, y1), (x2, y2), and (x3, y3) are the coordinates of the three points. If the area equals zero, the points are collinear. This method handles vertical lines gracefully.
Example: Using the same points A(1, 2), B(3, 4), and C(5, 6):
Area = 0.5 * |1(4 - 6) + 3(6 - 2) + 5(2 - 4)| = 0.5 * |-2 + 12 - 10| = 0
Since the area is 0, the points are collinear.
3. Using Vectors
Vector methods offer a powerful and elegant approach, particularly when dealing with higher dimensions. If the vectors formed by pairs of points are linearly dependent, the points are collinear. For three points A, B, and C, the vectors AB and AC are linearly dependent if AB = k * AC, where k is a scalar. This means that one vector is a scalar multiple of the other, implying that they lie on the same line.
4. Collinearity in Higher Dimensions
The principles of collinearity extend beyond two dimensions. In three dimensions (and higher), we can employ similar techniques involving vectors and determinants. For example, the scalar triple product of three vectors can be used to determine coplanarity (lying in the same plane); if the scalar triple product is zero, the vectors (and consequently the points they define) are coplanar. A set of points is collinear if they are coplanar and lie on a line within that plane.
Applications of Collinearity
The concept of collinearity is not just a theoretical curiosity; it has widespread applications in various fields:
1. Computer Graphics and Image Processing
Collinearity plays a crucial role in computer graphics algorithms for line detection, object recognition, and image analysis. Identifying collinear points helps in simplifying complex shapes and extracting meaningful features from images. For example, in edge detection, collinear points are crucial for defining straight edges in an image.
2. Spatial Analysis and Geographic Information Systems (GIS)
In GIS, identifying collinear points is essential for tasks such as road network analysis, determining spatial relationships between geographic features, and creating accurate maps. Analyzing collinear points helps in determining patterns and relationships within spatial data.
3. Surveying and Land Measurement
Surveying relies heavily on establishing collinearity between points to accurately measure distances and angles. The precise alignment of survey points ensures the accuracy of land measurements and mapping.
4. Physics and Engineering
Collinearity is important in various physical phenomena, such as determining the trajectory of projectiles, analyzing the equilibrium of forces, and understanding the motion of rigid bodies. For example, if three forces acting on a point are collinear, the net force on the point is simply the sum of the magnitudes of the individual forces.
5. Machine Learning and Data Analysis
Collinearity can be both a blessing and a curse in machine learning. While identifying collinear data points can be a useful way to understand relationships within a dataset, high collinearity among predictor variables in regression models can lead to instability and difficulty in interpretation.
Dealing with Imperfect Data and Noise
In real-world applications, data is often noisy or imperfect. Slight deviations from perfect collinearity may arise due to measurement errors, rounding errors, or inherent variability in the system. Therefore, a tolerance level or a threshold must be defined to account for these inaccuracies. Instead of strict equality to zero in the area calculation, we might check if the area is below a certain threshold. This practical approach allows for the identification of "near-collinear" points.
Advanced Concepts and Extensions
The study of collinearity extends to more advanced geometric concepts:
- Concurrent Lines: This concept deals with lines intersecting at a single point. Understanding collinearity is often a prerequisite for analyzing concurrent lines.
- Collineation: This term refers to a type of transformation that preserves collinearity; if points are collinear before the transformation, they remain collinear after the transformation.
- Projective Geometry: This branch of geometry heavily utilizes collinearity and projective transformations to analyze geometric relationships.
Conclusion
Collinearity, despite its seemingly simple definition, is a fundamental concept with profound implications across diverse fields. Mastering the techniques for determining collinearity, understanding its limitations in the presence of imperfect data, and appreciating its practical applications are essential for anyone working with geometrical data or spatial information. From computer graphics and GIS to physics and machine learning, the ability to identify and interpret collinear points remains a crucial skill in numerous computational and analytical tasks. This guide provides a comprehensive overview, equipping readers with the knowledge and tools necessary to effectively utilize this crucial geometrical concept.
Latest Posts
Latest Posts
-
Is The Square Root Of 24 A Rational Number
Apr 07, 2025
-
2550 50 100 20 100 100 600
Apr 07, 2025
-
Which One Of The Following Statements Is Not True
Apr 07, 2025
-
120 Sq Meters In Sq Feet
Apr 07, 2025
-
What Is The Common Multiple Of 12 And 16
Apr 07, 2025
Related Post
Thank you for visiting our website which covers about Points Lie On The Same Line . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.