Negative 15 Square Root Divided By Negaitve Square Root 3
Juapaving
May 10, 2025 · 5 min read
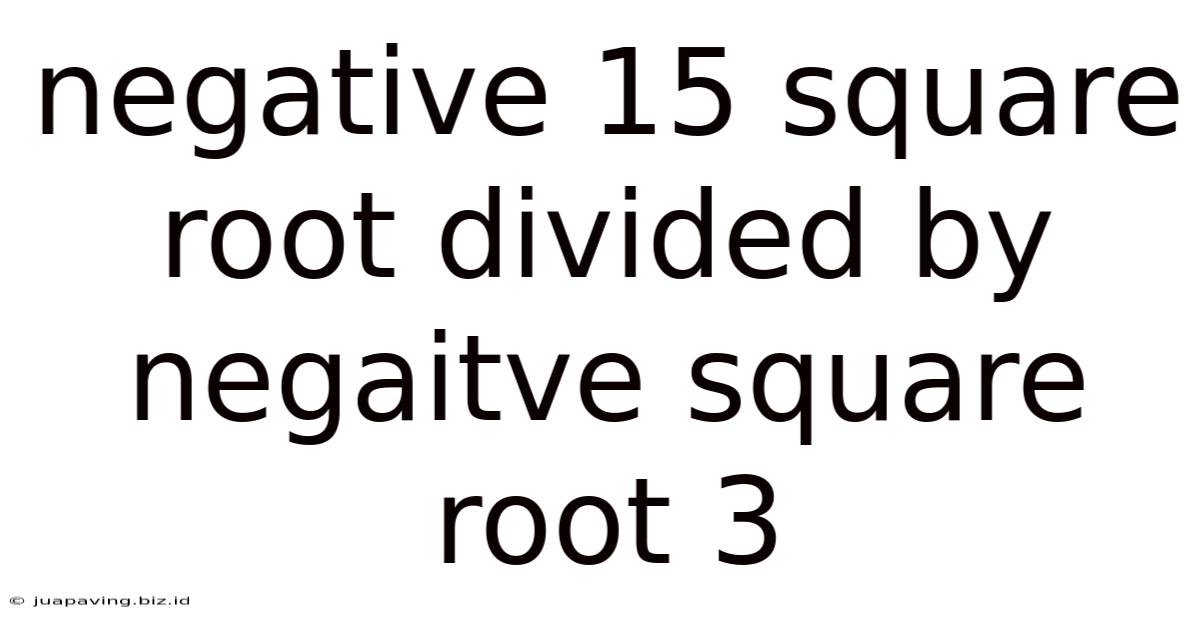
Table of Contents
Deconstructing the Expression: √(-15) / √(-3)
This article delves into the intricacies of the mathematical expression √(-15) / √(-3), providing a comprehensive explanation of its solution, encompassing complex numbers, simplification techniques, and relevant mathematical concepts. We'll explore the process step-by-step, highlighting important considerations and potential pitfalls along the way.
Understanding Complex Numbers
Before we embark on solving √(-15) / √(-3), we must first establish a firm grasp of complex numbers. Real numbers, which we encounter in everyday life, can be represented on a number line. However, complex numbers extend beyond the real number line by incorporating the imaginary unit, denoted as 'i'. This imaginary unit is defined as the square root of -1: i = √(-1).
Complex numbers are expressed in the form a + bi, where 'a' is the real part and 'b' is the imaginary part. In our expression, both the numerator and denominator involve the square root of negative numbers, indicating the presence of imaginary components.
Breaking Down the Numerator: √(-15)
The numerator, √(-15), involves the square root of a negative number. We can rewrite this using the imaginary unit 'i':
√(-15) = √(-1 * 15) = √(-1) * √(15) = i√15
Notice that we've separated the negative sign from the radicand (the number inside the square root). This allows us to express the square root of -1 as 'i', leaving us with i√15 – a complex number with a real part of 0 and an imaginary part of √15.
Addressing the Denominator: √(-3)
Similarly, the denominator, √(-3), can be expressed using the imaginary unit:
√(-3) = √(-1 * 3) = √(-1) * √(3) = i√3
Again, we separate the negative sign, expressing the square root of -1 as 'i', leaving us with i√3.
Simplifying the Expression: (i√15) / (i√3)
Now that we've expressed both the numerator and denominator in terms of 'i', we can rewrite the original expression as:
(i√15) / (i√3)
Notice that 'i' appears in both the numerator and the denominator. We can cancel these out, simplifying the expression:
(i√15) / (i√3) = √15 / √3
This simplification is crucial because it reduces the complexity of the expression and allows us to proceed with further simplification.
Rationalizing and Final Result
The expression is now in a simpler form: √15 / √3. To simplify this further, we can use the properties of radicals:
√(a/b) = √a / √b and √a * √a = a
Applying these properties:
√15 / √3 = √(15/3) = √5
Therefore, the solution to the original expression, √(-15) / √(-3), is √5. This is a real number, even though our initial expression involved complex numbers. The cancellation of the imaginary units 'i' in the numerator and denominator leads to a real number solution.
Advanced Considerations: Complex Number Arithmetic
While we successfully simplified the expression, it's crucial to understand that this simplification relies on the specific structure of the expression. Dividing complex numbers in general is not as straightforward as cancelling out common factors in the imaginary units. Let’s examine a slightly different approach which highlights the importance of complex number arithmetic:
We can rewrite the original expression using the polar form of complex numbers. This form is particularly useful for division and multiplication of complex numbers.
The rectangular form of a complex number is a + bi. The polar form is r(cos θ + i sin θ), where r is the modulus (or magnitude) and θ is the argument (or angle).
- Converting to Polar Form:
First, we need to convert our complex numbers i√15 and i√3 into their polar forms. For i√15:
- Modulus (r): √((0)² + (√15)²) = √15
- Argument (θ): arctan(√15/0) = π/2 (since the real part is 0 and the imaginary part is positive)
Thus, i√15 in polar form is √15(cos(π/2) + i sin(π/2)).
Similarly, for i√3:
- Modulus (r): √((0)² + (√3)²) = √3
- Argument (θ): arctan(√3/0) = π/2
Thus, i√3 in polar form is √3(cos(π/2) + i sin(π/2)).
- Division in Polar Form:
Dividing two complex numbers in polar form involves dividing their moduli and subtracting their arguments:
[√15(cos(π/2) + i sin(π/2))] / [√3(cos(π/2) + i sin(π/2))] = (√15/√3)[cos(π/2 - π/2) + i sin(π/2 - π/2)] = √5(cos(0) + i sin(0)) = √5
- Converting Back to Rectangular Form:
√5(cos(0) + i sin(0)) = √5(1 + 0i) = √5
This confirms our previous result. Although the polar form might seem more complex initially, it provides a more rigorous method for handling complex number division, especially when dealing with complex numbers with non-zero real parts.
Avoiding Common Mistakes
Several common mistakes can arise when dealing with complex numbers:
- Incorrect use of the imaginary unit 'i': Remember that i² = -1. Failing to account for this can lead to significant errors in calculations.
- Improper simplification of radicals: Ensure you correctly simplify radical expressions before proceeding with further calculations.
- Ignoring the order of operations: Follow the order of operations (PEMDAS/BODMAS) correctly to avoid incorrect results.
Conclusion
Solving √(-15) / √(-3) requires a solid understanding of complex numbers and their properties. By carefully applying the rules of complex number arithmetic and simplification techniques, we arrive at the solution √5. This article provided a detailed step-by-step approach to solving the expression, highlighting the critical steps involved and discussing advanced techniques like using the polar form of complex numbers for a more robust and generalizable approach. Remember to always meticulously follow the rules of mathematics and carefully check your work to avoid common pitfalls. This careful and thorough approach is crucial for accurate and meaningful results in mathematics, particularly when working with complex numbers.
Latest Posts
Latest Posts
-
According To Mendels Law Of Independent Assortment
May 10, 2025
-
Chemical Element With Atomic Number 1
May 10, 2025
-
What Does Reticular Tissue Look Like
May 10, 2025
-
How Many Moles In 1l Of Water
May 10, 2025
-
Differences Between Meiosis 1 And Meiosis 2
May 10, 2025
Related Post
Thank you for visiting our website which covers about Negative 15 Square Root Divided By Negaitve Square Root 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.