Lowest Common Multiple Of 15 And 25
Juapaving
Apr 01, 2025 · 5 min read
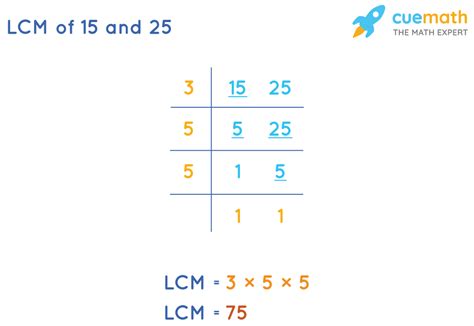
Table of Contents
- Lowest Common Multiple Of 15 And 25
- Table of Contents
- Finding the Lowest Common Multiple (LCM) of 15 and 25: A Comprehensive Guide
- Understanding Lowest Common Multiple (LCM)
- Methods for Finding the LCM of 15 and 25
- 1. Listing Multiples Method
- 2. Prime Factorization Method
- 3. Greatest Common Divisor (GCD) Method
- Applications of LCM
- Further Exploration of LCM and Related Concepts
- Conclusion
- Latest Posts
- Latest Posts
- Related Post
Finding the Lowest Common Multiple (LCM) of 15 and 25: A Comprehensive Guide
The lowest common multiple (LCM) is a fundamental concept in mathematics, particularly in number theory and arithmetic. Understanding how to calculate the LCM is crucial for solving various mathematical problems, from simplifying fractions to tackling more complex algebraic equations. This article delves into the methods for finding the LCM of 15 and 25, providing a detailed explanation and exploring different approaches to this seemingly simple yet insightful mathematical operation. We'll also explore the broader context of LCM and its applications.
Understanding Lowest Common Multiple (LCM)
Before diving into the specifics of finding the LCM of 15 and 25, let's establish a clear understanding of what the LCM represents. The LCM of two or more integers is the smallest positive integer that is divisible by all the integers without leaving a remainder. In simpler terms, it's the smallest number that is a multiple of all the given numbers.
For example, consider the numbers 2 and 3. The multiples of 2 are 2, 4, 6, 8, 10, 12, 14, 16, 18... and the multiples of 3 are 3, 6, 9, 12, 15, 18... The smallest number that appears in both lists is 6. Therefore, the LCM of 2 and 3 is 6.
Methods for Finding the LCM of 15 and 25
Several methods can be employed to determine the LCM of 15 and 25. Let's explore three common approaches:
1. Listing Multiples Method
This is a straightforward method, particularly useful for smaller numbers. We list the multiples of each number until we find the smallest common multiple.
- Multiples of 15: 15, 30, 45, 60, 75, 90, 105, 120, 135, 150...
- Multiples of 25: 25, 50, 75, 100, 125, 150...
By examining the lists, we observe that the smallest number present in both sequences is 75. Therefore, the LCM of 15 and 25 is 75.
This method is simple but can become cumbersome for larger numbers. Imagine trying to find the LCM of, say, 144 and 288 using this method; it would be extremely time-consuming. Hence, more efficient methods are required for larger numbers.
2. Prime Factorization Method
This method utilizes the prime factorization of each number. It's a more efficient and systematic approach, especially when dealing with larger numbers.
First, we find the prime factorization of 15 and 25:
- 15 = 3 x 5
- 25 = 5 x 5 = 5²
Next, we identify the highest power of each prime factor present in the factorizations:
- The highest power of 3 is 3¹
- The highest power of 5 is 5²
Finally, we multiply these highest powers together to obtain the LCM:
LCM(15, 25) = 3¹ x 5² = 3 x 25 = 75
This method is significantly more efficient than the listing multiples method, especially when dealing with larger numbers. It provides a structured and reliable way to calculate the LCM.
3. Greatest Common Divisor (GCD) Method
This method leverages the relationship between the LCM and the greatest common divisor (GCD) of two numbers. The GCD is the largest positive integer that divides both numbers without leaving a remainder. The relationship between the LCM and GCD is given by the formula:
LCM(a, b) = (|a x b|) / GCD(a, b)
where 'a' and 'b' are the two numbers.
First, let's find the GCD of 15 and 25 using the Euclidean algorithm:
- Divide the larger number (25) by the smaller number (15): 25 ÷ 15 = 1 with a remainder of 10.
- Replace the larger number with the smaller number (15) and the smaller number with the remainder (10): 15 ÷ 10 = 1 with a remainder of 5.
- Repeat the process: 10 ÷ 5 = 2 with a remainder of 0.
The last non-zero remainder is the GCD, which is 5.
Now, we can use the formula to calculate the LCM:
LCM(15, 25) = (15 x 25) / 5 = 375 / 5 = 75
This method, while involving an extra step of finding the GCD, provides an alternative and equally effective approach to determining the LCM. The Euclidean algorithm for finding the GCD is particularly efficient for larger numbers.
Applications of LCM
The concept of LCM has wide-ranging applications across various mathematical fields and real-world scenarios. Some key applications include:
-
Fraction Addition and Subtraction: Finding a common denominator when adding or subtracting fractions requires determining the LCM of the denominators.
-
Scheduling Problems: Determining when events will coincide, such as the overlapping of bus schedules or the synchronization of machinery, often involves finding the LCM of the time intervals.
-
Number Theory: LCM plays a crucial role in solving problems related to divisibility, modular arithmetic, and other number-theoretic concepts.
-
Music Theory: The LCM is used to calculate the least common period of musical notes with different rhythmic values.
-
Computer Science: The LCM concept finds applications in algorithms dealing with cycle detection, synchronization, and data structures.
Further Exploration of LCM and Related Concepts
For a deeper understanding, you can explore more advanced concepts related to LCM, such as:
-
LCM of more than two numbers: The methods described above can be extended to find the LCM of three or more numbers. The prime factorization method is particularly well-suited for this.
-
Least Common Multiple and Greatest Common Divisor (GCD) Relationship: Further study of the intricate relationship between LCM and GCD will provide valuable insights into number theory. Exploring the Euclidean algorithm and its variations is highly recommended.
-
Modular Arithmetic and LCM: Understanding the application of LCM in solving congruence equations and other problems in modular arithmetic provides a rewarding extension of the LCM concept.
Conclusion
Finding the lowest common multiple of 15 and 25, while seemingly simple, provides a gateway to understanding a crucial mathematical concept with broad applications. We explored three methods – listing multiples, prime factorization, and the GCD method – each offering different levels of efficiency. The choice of method depends on the context and the size of the numbers involved. The prime factorization method generally provides the most efficient and systematic approach, particularly for larger numbers. Understanding the LCM is essential not only for solving mathematical problems but also for tackling real-world scenarios requiring the synchronization of events or the simplification of calculations involving fractions. By grasping this fundamental concept, you expand your mathematical toolkit and open up opportunities for exploring more advanced mathematical ideas.
Latest Posts
Latest Posts
-
Cellulose Cannot Be Digested By Humans
Apr 05, 2025
-
A Thin Uniform Rod Of Length L
Apr 05, 2025
-
5 Letter Word Ends With Eat
Apr 05, 2025
-
The Law Of Diminishing Marginal Utility States That
Apr 05, 2025
Related Post
Thank you for visiting our website which covers about Lowest Common Multiple Of 15 And 25 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
