List The Numbers That Have 30 As A Multiple
Juapaving
Mar 24, 2025 · 4 min read
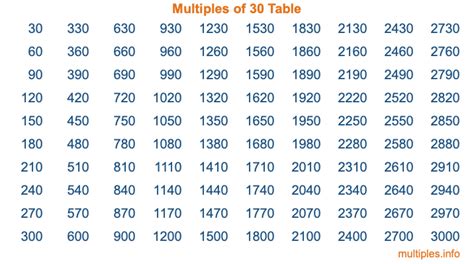
Table of Contents
Listing Numbers That Have 30 as a Multiple: A Deep Dive into Divisibility and Factors
Finding all the numbers that have 30 as a multiple might seem like a simple task at first glance. However, exploring this seemingly straightforward question opens a door to understanding fundamental concepts in mathematics, including divisibility rules, prime factorization, and the fascinating world of factors and multiples. This article will not only provide a comprehensive list (within practical limits) but also delve into the theoretical underpinnings that make this possible.
Understanding Multiples and Divisibility
Before we embark on listing numbers with 30 as a multiple, let's solidify our understanding of key terms.
Multiple: A multiple of a number is the product of that number and any integer (whole number). For example, multiples of 3 include 3, 6, 9, 12, 15, and so on.
Divisor (or Factor): A divisor of a number is an integer that divides the number without leaving a remainder. For example, the divisors of 12 are 1, 2, 3, 4, 6, and 12.
The relationship between multiples and divisors is inverse. If 'a' is a multiple of 'b', then 'b' is a divisor of 'a'. Conversely, if 'b' is a divisor of 'a', then 'a' is a multiple of 'b'. Therefore, finding numbers that have 30 as a multiple is equivalent to finding multiples of 30.
Generating Multiples of 30: The Systematic Approach
The most straightforward way to list numbers that have 30 as a multiple is to systematically multiply 30 by each integer:
- 30 x 1 = 30
- 30 x 2 = 60
- 30 x 3 = 90
- 30 x 4 = 120
- 30 x 5 = 150
- 30 x 6 = 180
- 30 x 7 = 210
- 30 x 8 = 240
- 30 x 9 = 270
- 30 x 10 = 300
- ...and so on, infinitely.
This method generates an infinite sequence of numbers, all of which are multiples of 30. Practically, we can't list them all. However, we can explore the pattern and properties of these numbers.
Prime Factorization: Unveiling the Building Blocks
To gain deeper insight, let's consider the prime factorization of 30. Prime factorization involves expressing a number as a product of prime numbers (numbers divisible only by 1 and themselves). The prime factorization of 30 is 2 x 3 x 5.
This factorization is crucial because it reveals the fundamental building blocks of all multiples of 30. Any multiple of 30 must contain at least one factor of 2, one factor of 3, and one factor of 5.
Implications of Prime Factorization
Understanding the prime factorization allows us to identify numbers that cannot be multiples of 30. For instance, any number lacking a factor of 2, 3, or 5 cannot be a multiple of 30.
This insight helps us efficiently filter potential candidates when searching for multiples of 30.
Divisibility Rules: Shortcuts to Identification
Divisibility rules offer quick checks to determine if a number is divisible by another. For 30, we can combine divisibility rules for 2, 3, and 5:
- Divisibility by 2: The number must be even (last digit is 0, 2, 4, 6, or 8).
- Divisibility by 3: The sum of the digits must be divisible by 3.
- Divisibility by 5: The number must end in 0 or 5.
A number is divisible by 30 only if it satisfies all three rules. This provides a significantly faster way to test whether a given number is a multiple of 30 than performing long division.
Exploring Patterns in Multiples of 30
The sequence of multiples of 30 (30, 60, 90, 120, ...) exhibits several interesting patterns:
-
Arithmetic Progression: The sequence forms an arithmetic progression with a common difference of 30. This means that each term is obtained by adding 30 to the previous term.
-
Divisibility by Factors of 30: All multiples of 30 are also divisible by 1, 2, 3, 5, 6, 10, 15, and of course, 30. This stems directly from the factors of 30.
-
Last Digit Pattern: The last digits of multiples of 30 alternate between 0.
Practical Applications and Real-World Examples
The concept of multiples and divisors finds applications in many areas:
-
Scheduling and Time Management: Multiples of 30 are frequently used in scheduling appointments, events, and tasks (e.g., 30-minute intervals).
-
Measurement and Units: Multiples of 30 appear in various units of measurement (e.g., 30 days in a month, approximately).
-
Geometry and Number Theory: Multiples of 30 play a role in geometric problems and number theory theorems.
Conclusion: The Enduring Significance of Multiples
While the seemingly simple question of listing numbers that have 30 as a multiple leads to an infinite sequence, exploring the underlying mathematical concepts provides a rich understanding of divisibility, factors, prime factorization, and patterns in number sequences. The ability to efficiently identify and generate multiples is valuable in various fields, showcasing the enduring significance of these fundamental mathematical ideas. From scheduling appointments to advanced mathematical theorems, the concept of multiples and divisors continues to be a cornerstone of mathematical understanding and application. By applying the methods outlined in this article – systematic multiplication, prime factorization, and divisibility rules – one can confidently tackle similar problems involving multiples of other numbers. Remember, the seemingly simple often holds hidden depths of mathematical elegance and practicality.
Latest Posts
Latest Posts
-
Vidhan Sabha Vs Lok Sabha Vs Rajya Sabha
Mar 29, 2025
-
What Can 81 Be Divided By
Mar 29, 2025
-
A Number Is Divisible By 6 If
Mar 29, 2025
-
What Stores Water In Plant Cells
Mar 29, 2025
-
Exercise On Transitive And Intransitive Verbs
Mar 29, 2025
Related Post
Thank you for visiting our website which covers about List The Numbers That Have 30 As A Multiple . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
