Least Common Multiple Of 12 15
Juapaving
Mar 28, 2025 · 5 min read
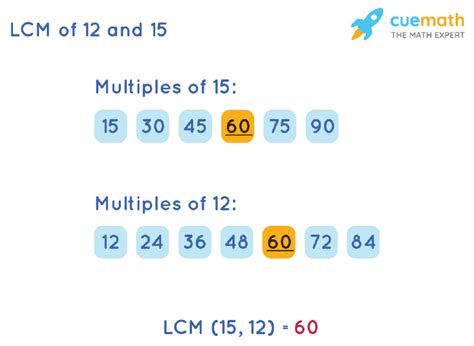
Table of Contents
Finding the Least Common Multiple (LCM) of 12 and 15: A Comprehensive Guide
The least common multiple (LCM) is a fundamental concept in mathematics, particularly in number theory and arithmetic. Understanding how to find the LCM is crucial for various applications, from simplifying fractions to solving problems in algebra and beyond. This article delves deep into the methods of calculating the LCM, focusing specifically on finding the least common multiple of 12 and 15, while also providing a broader understanding of the concept and its applications.
What is the Least Common Multiple (LCM)?
The least common multiple (LCM) of two or more integers is the smallest positive integer that is divisible by all the integers. In simpler terms, it's the smallest number that all the given numbers can divide into evenly. For instance, the LCM of 2 and 3 is 6 because 6 is the smallest positive integer that is divisible by both 2 and 3.
Methods for Finding the LCM
Several methods exist for calculating the LCM. Let's explore the most common approaches, illustrating them with the example of finding the LCM of 12 and 15:
1. Listing Multiples Method
This method is straightforward but can be time-consuming for larger numbers. It involves listing the multiples of each number until you find the smallest common multiple.
- Multiples of 12: 12, 24, 36, 48, 60, 72, ...
- Multiples of 15: 15, 30, 45, 60, 75, ...
The smallest multiple that appears in both lists is 60. Therefore, the LCM of 12 and 15 is 60.
2. Prime Factorization Method
This method is generally more efficient, especially for larger numbers. It involves finding the prime factorization of each number and then constructing the LCM from the prime factors.
- Prime factorization of 12: 2² × 3
- Prime factorization of 15: 3 × 5
To find the LCM, we take the highest power of each prime factor present in either factorization:
- Highest power of 2: 2² = 4
- Highest power of 3: 3¹ = 3
- Highest power of 5: 5¹ = 5
Multiply these highest powers together: 4 × 3 × 5 = 60. Therefore, the LCM of 12 and 15 is 60.
3. Greatest Common Divisor (GCD) Method
This method utilizes the relationship between the LCM and the greatest common divisor (GCD) of two numbers. The product of the LCM and GCD of two numbers is always equal to the product of the two numbers. The formula is:
LCM(a, b) × GCD(a, b) = a × b
First, we need to find the GCD of 12 and 15. We can use the Euclidean algorithm for this:
- Divide the larger number (15) by the smaller number (12): 15 ÷ 12 = 1 with a remainder of 3.
- Replace the larger number with the smaller number (12) and the smaller number with the remainder (3): 12 ÷ 3 = 4 with a remainder of 0.
- Since the remainder is 0, the GCD is the last non-zero remainder, which is 3.
Now, we can use the formula:
LCM(12, 15) × GCD(12, 15) = 12 × 15 LCM(12, 15) × 3 = 180 LCM(12, 15) = 180 ÷ 3 = 60
Therefore, the LCM of 12 and 15 is 60.
Understanding the Significance of the LCM
The LCM has numerous applications across various mathematical fields and real-world scenarios:
-
Fraction Addition and Subtraction: Finding a common denominator when adding or subtracting fractions requires determining the LCM of the denominators. For example, to add 1/12 and 1/15, we need to find the LCM of 12 and 15, which is 60. Then we can rewrite the fractions as 5/60 and 4/60, respectively, allowing for easy addition.
-
Cyclic Events: The LCM is useful in problems involving repeating events that occur at different intervals. For instance, if two machines cycle every 12 minutes and 15 minutes respectively, the LCM (60 minutes) represents the time when both machines will cycle simultaneously again.
-
Modular Arithmetic: LCM plays a crucial role in modular arithmetic, which involves operations with remainders. For example, it's essential in solving congruences.
-
Scheduling and Planning: In project management or scheduling problems, determining the LCM of different task durations can help optimize timelines and resource allocation.
LCM of Larger Numbers and Multiple Numbers
While the methods discussed above are applicable to any number of integers, the prime factorization method becomes increasingly efficient for larger numbers. For instance, finding the LCM of three numbers, say 12, 15, and 20, involves finding the prime factorization of each number and then selecting the highest power of each prime factor present:
- 12 = 2² × 3
- 15 = 3 × 5
- 20 = 2² × 5
The LCM is then 2² × 3 × 5 = 60.
For multiple numbers, the process remains the same: find the prime factorization of each number and then take the highest power of each prime factor that appears in any of the factorizations.
Practical Applications and Real-World Examples
Beyond the mathematical realm, the LCM finds practical applications in various everyday situations:
-
Music Theory: In music, the LCM is used to determine the least common multiple of two or more rhythmic patterns, helping musicians coordinate their performances.
-
Construction and Engineering: The LCM is used in construction and engineering to determine optimal material lengths or time intervals for various tasks, optimizing efficiency and minimizing waste.
-
Data Synchronization: In computer science, synchronizing data from different sources often relies on the LCM to find the smallest common interval for updates.
-
Manufacturing: Production lines with machines operating at different cycles can utilize the LCM to coordinate their operations and maximize output.
Advanced Concepts and Extensions
The concept of the LCM extends to more advanced mathematical contexts such as:
-
Abstract Algebra: The concept of LCM is generalized in abstract algebra to ideals in rings.
-
Number Theory: The LCM is used in various number-theoretic problems, such as solving Diophantine equations.
Conclusion
Understanding and calculating the LCM is an essential skill in mathematics with far-reaching applications across numerous fields. Whether you use the listing multiples method, the prime factorization method, or the GCD method, the core principle remains consistent: finding the smallest positive integer divisible by all the given numbers. The LCM of 12 and 15, as demonstrated through different methods, is 60, a number that plays a crucial role in various mathematical and real-world scenarios. Mastering the LCM opens doors to more advanced mathematical concepts and solutions to practical problems. By understanding its significance and diverse applications, we appreciate its importance in both theoretical and applied mathematics.
Latest Posts
Latest Posts
-
Which Of The Following Processes Returns Carbon To The Atmosphere
Mar 31, 2025
-
5 Letter Word That Starts With Vi
Mar 31, 2025
-
Can Acquired Characteristics Be Passed On The Next Generation
Mar 31, 2025
-
What Are The Three Body Parts Of A Mollusk
Mar 31, 2025
-
How Many Feet Is 45 Inches
Mar 31, 2025
Related Post
Thank you for visiting our website which covers about Least Common Multiple Of 12 15 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
