Least Common Multiple 10 And 15
Juapaving
May 14, 2025 · 5 min read
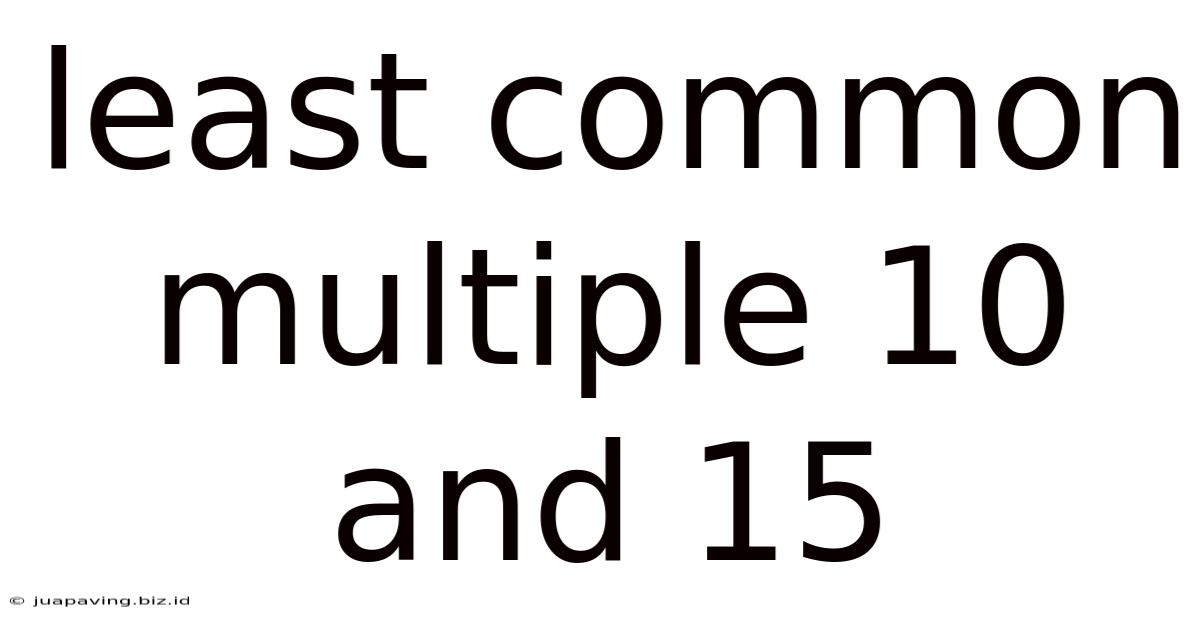
Table of Contents
Finding the Least Common Multiple (LCM) of 10 and 15: A Comprehensive Guide
The least common multiple (LCM) is a fundamental concept in mathematics with wide-ranging applications in various fields, from scheduling problems to music theory. Understanding how to find the LCM is crucial for anyone working with numbers, fractions, and ratios. This article delves into the process of determining the LCM of 10 and 15, exploring different methods and providing a thorough understanding of the underlying principles. We'll also touch upon the significance of the LCM and its real-world applications.
Understanding Least Common Multiple (LCM)
Before we jump into calculating the LCM of 10 and 15, let's define the term. The least common multiple of two or more integers is the smallest positive integer that is divisible by all the integers. In simpler terms, it's the smallest number that all the given numbers can divide into evenly without leaving a remainder.
For example, let's consider the numbers 2 and 3. The multiples of 2 are 2, 4, 6, 8, 10, 12, and so on. The multiples of 3 are 3, 6, 9, 12, 15, and so on. The common multiples of 2 and 3 are 6, 12, 18, etc. The smallest of these common multiples is 6, therefore, the LCM of 2 and 3 is 6.
Methods for Finding the LCM of 10 and 15
There are several effective methods to determine the LCM of two numbers, including 10 and 15. Let's explore the most common techniques:
1. Listing Multiples Method
This is a straightforward approach, particularly useful for smaller numbers. We list the multiples of each number until we find the smallest common multiple.
Multiples of 10: 10, 20, 30, 40, 50, 60... Multiples of 15: 15, 30, 45, 60, 75...
By comparing the lists, we can see that the smallest common multiple of 10 and 15 is 30. Therefore, the LCM(10, 15) = 30. This method is intuitive but can become cumbersome for larger numbers.
2. Prime Factorization Method
This method is more efficient, especially for larger numbers. It involves finding the prime factorization of each number and then constructing the LCM using the highest powers of each prime factor present.
Prime factorization of 10: 2 x 5 Prime factorization of 15: 3 x 5
To find the LCM, we take the highest power of each prime factor present in the factorizations:
- The prime factors are 2, 3, and 5.
- The highest power of 2 is 2¹ = 2
- The highest power of 3 is 3¹ = 3
- The highest power of 5 is 5¹ = 5
Therefore, LCM(10, 15) = 2 x 3 x 5 = 30
This method is more systematic and efficient than listing multiples, especially when dealing with larger numbers with many factors.
3. Greatest Common Divisor (GCD) Method
The LCM and GCD (greatest common divisor) of two numbers are related. We can use the following formula:
LCM(a, b) x GCD(a, b) = a x b
First, let's find the GCD of 10 and 15 using the Euclidean algorithm:
- Divide the larger number (15) by the smaller number (10): 15 ÷ 10 = 1 with a remainder of 5.
- Replace the larger number with the smaller number (10) and the smaller number with the remainder (5): 10 ÷ 5 = 2 with a remainder of 0.
- The GCD is the last non-zero remainder, which is 5. Therefore, GCD(10, 15) = 5.
Now, we can use the formula:
LCM(10, 15) = (10 x 15) / GCD(10, 15) = (150) / 5 = 30
This method efficiently utilizes the relationship between LCM and GCD.
Applications of LCM
The concept of the least common multiple has numerous real-world applications across various disciplines:
1. Scheduling and Time Management
Imagine you have two events that occur at regular intervals. One event happens every 10 days, and another happens every 15 days. To find out when both events will occur simultaneously, you need to find the LCM of 10 and 15, which is 30. Both events will coincide every 30 days. This principle is applicable to scheduling meetings, production cycles, and numerous other time-related scenarios.
2. Fraction Operations
The LCM plays a crucial role in adding and subtracting fractions. To add or subtract fractions with different denominators, you need to find the LCM of the denominators. This LCM becomes the common denominator, simplifying the addition or subtraction process. For instance, to add 1/10 and 1/15, you would find the LCM of 10 and 15 (which is 30) and then convert the fractions to have a common denominator of 30 before adding them.
3. Music Theory
Musical intervals and rhythms often involve the LCM. For example, if one musical phrase repeats every 10 beats and another every 15 beats, the LCM (30) determines when both phrases will align perfectly, creating a harmonious pattern.
4. Gear Ratios and Engineering
In mechanical systems with gears, the LCM is used to calculate the speed ratios and timing of rotating components. Understanding the LCM helps engineers optimize the performance and synchronicity of mechanical systems.
5. Cyclic Processes
Many natural and man-made processes are cyclic, repeating at regular intervals. Finding the LCM can be essential to understand when different cyclic processes will coincide or align. This is relevant in various fields like physics, chemistry, and even biology.
Conclusion: Mastering the LCM of 10 and 15 and Beyond
This comprehensive guide has demonstrated different methods for calculating the least common multiple, focusing specifically on the example of 10 and 15. While the listing multiples method offers a simple approach for smaller numbers, the prime factorization and GCD methods are more efficient and versatile for tackling larger or more complex problems. Understanding the LCM is not just about solving mathematical problems; it’s about developing a deeper understanding of numerical relationships and applying this knowledge to solve real-world problems in various fields. By mastering the concept of LCM, you expand your mathematical toolbox and enhance your problem-solving capabilities significantly. Remember that the key to success is practice and a thorough understanding of the underlying principles. The more you practice, the more comfortable you'll become with applying these techniques to various scenarios and numbers.
Latest Posts
Latest Posts
-
Is Cellular Respiration Exothermic Or Endothermic
May 14, 2025
-
Common Multiples Of 4 And 6
May 14, 2025
-
5 Letter Word Starting With H A
May 14, 2025
-
Describing Words That Begin With O
May 14, 2025
-
5 Letter Words Starting With Roo
May 14, 2025
Related Post
Thank you for visiting our website which covers about Least Common Multiple 10 And 15 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.